数量关系
1 小注意点
1、1不是质数
2、东南西北方向是?如下
2 主要内容
三大方法:代入排除法、倍数特性法、方程法
六大题型:工程问题、经济利润
行程问题、几何问题
排列组合与概率、容斥原理
周期问题、最值问题、溶液问题、牛吃草问题等小考点会在后续的(粉笔980 2025)强化练习课、真题课、学霸养成课补充讲解
补充:线段法,如例2(P195,解题方法在“4 倍数特性法”的博客4)
3 代入排除法
1、什么时候用?
(1)看选项
选项信息充分:选项为一组数。此时选项把每个要求的数都给我们了,就用代入排除法
(2)看题型
出现特定题型:年龄、余数、多位数、不定方程
① 年龄:涉及到年龄的问题
② 余数:出现“多”、“剩”、“余”、“缺”等关键字
例:一个数,除以7余3,除以8余2,除以9余1.
A. 10 B.11
③ 多位数:出现位数的变化
例:多个三位数,十位和个位对调,比原来大9
A.121 B.123
④ 不定方程:后面方程法单独讲解
2、注意点
(1)求至少,要从最小的选项开始代入,因为有可能很多个选项都符合,但题目是求最少的那个选项
3、对于例3(P193),我有话要说,就是这题不用代入法写,得设边长为$x$,则$x^2(x-2)=144$,属于高次方程。
我们行测需要求解的基本是一元一次方程、二元一次方程等这种很好求解的方程组。对于像例3(P193)需要求解高次方程的题,可以不用硬解,直接代入选项即可!!!
4 倍数特性法(行测里最好用的排除选项的方法)
1、关于倍数特性法:
$\bigstar$此方法基于的基础知识:
如果$A=B\times C$,($B$、$C$均为整数)。那么,$A$能被$B$整除,且$A$能被$C$整除
此基础知识可以写题:
(2021北京)为响应国家“做好重点群体就业工作”的号召,某企业扩大招聘规模,计划在年内招聘高校毕业生240名,但实际招聘的高校毕业生数量多于计划招聘的数量。已知企业将招聘到的高校毕业生平均分配到7个部门培训,并在培训结束后将他们平均分配到9个分公司工作。问该企业实际招聘的高校毕业生至少比计划招聘数多多少人?
A. 6
B. 12
C. 14
D. 28
这个题选什么?
选B。因为实际招聘的数量能被7和9整除,则实际招聘数量能被63整除。因为实际招聘数量>240,而63*3<240,63*4刚好大于240,则至少招聘了63*4=252人,则多252-240=12人。此题思维:出现平均分考虑倍数关系
$\bigstar$以上习题涉及整数判定,整除判定技巧如下
(1)口诀法:
3、9看各位数字之和(如657能不能被9整除?6+5+7=18,18能被9整除,因此657能被9整除);
5看末位(末位为0、5就能被5整除);
4看末两位(如624只需要看末两位24,24能被4整除,则624能被4整除;因为624=600+24,而100一定是4的倍数,因此不用管600,只需要看24,即看末两位)
(2)因式分解:
判断x是否能被18整除,只需要判断x是否能同时被2、9整除
因式分解后的2个数字必须互质(即没有公约数),如这里提到的18分解的2个数字为2、9
(3)拆分法:
判断x是否能被7整除,可以把x拆成7的倍数$\pm$零头,只看零头能否被7整除
如644=630+14,就看14能不能被7整除,发现可以,那么644能被7整除
又如判断354能被18整除不,而354=360-6,6不能被18整除,则354不能被18整除
$\bigstar$什么时候考虑倍数特性法?
(1)出现“平均分”(暗含平均分的字:每、循环报数)、余数等字眼则考虑倍数关系,对应“余数型”的题型;
(2)出现比例如30%(即可以化成比例3:10)、$\frac{5}{9}$、5:3、2.5倍(即2.5:1=5:2)等的时候,对应“比例型”的题型;
(3)给数值范围和比例关系,没给具体值,但问具体值,一般都是考倍数特性法,通过倍数关系确定具体值。
$\bigstar$题型:
(1)余数型
(2)比例型
①基础知识:
如果$\frac{A}{B}=\frac{m}{n}$(m与n互质,即m和n需要化成最简整数比)
那么,A是m的倍数
B是n的倍数
A+B是m+n的倍数
A-B是m-n的倍数
扩展:如果C比D多$\frac{x}{y}$,则$\frac{C}{D}=1+\frac{x}{y}=\frac{x+y}{y}$
②什么时候用?
出现比例如30%(即可以化成比例3:10)、$\frac{5}{9}$、5:3、2.5倍(即2.5:1=5:2)的时候
③比例型做题思路总结:
情况1:根据$\frac{A}{B}=\frac{m}{n}$的m和n的倍数求出选项。求总人数的题,有个条件说“20岁以下的人数占总人数的68%”,即占总人数的$\frac{68}{100}=\frac{17}{25}$,即总人数可以被25整除;
情况2:根据$\frac{A}{B}=1+\frac{m}{n}=\frac{m+n}{n}$的m+n的倍数和n的倍数求出选项。求B品牌去年生产的数量。已知B品牌去年比前年多生产15%,则$\frac{去年}{前年}=1+15\%=1+\frac{3}{20}=\frac{23}{20}$,则去年生产的数量是23的倍数;
情况3:间接求法。求今年推荐录取的人数。已知今年共录取231个硕士研究生,其中推荐录取的人数比去年减少$\frac{1}{6}$,考试录取的人数比去年增加
$\frac{31}{150}$,则$\frac{今年推荐}{去年推荐}=1-\frac{1}{6}=\frac{5}{6}$,$\frac{今年考试}{去年考试}=1+\frac{31}{150}=\frac{181}{150}$,则今年推荐是5的倍数,今年考试是181的倍数,代入A.今年推荐40人,则今年考试人数为231-40=191,不是181的倍数;代入C.今年推荐50人,则今年考试231-50=181人,是181的倍数,则选C;
情况4:直接计算。例4(P195),看下面的博客6;
情况5:根据$\frac{A}{B}=\frac{m}{n}$可以推出$\frac{A}{A+B}=\frac{m}{m+n}$,根据A+B是m+n的倍数来求出选项。如求参与投票的总人数,最初支持方案A的人数比支持方案B的人数多$\frac{1}{4}$,则$\frac{A}{B}=\frac{5}{4}$,则总人数是9的倍数,则选出只有选项C.90是9的倍数;
情况6:根据$\frac{A}{B}=\frac{m}{n}$可以推出$\frac{A}{A-B}=\frac{m}{m-n}$,根据A-B是m-n的倍数来求出选项。如不到30岁的哥哥今年的年龄正好是弟弟年龄的5倍,若干年后哥哥的年龄就是弟弟的4倍,又过了若干年,哥哥的年龄将是弟弟的3倍,求今年两兄弟的年龄差。今年$\frac{哥}{弟}=\frac{5}{1}$,则年龄差是4的倍数;若干年$\frac{哥}{弟}=\frac{4}{1}$,则年龄差是3的倍数;又过若干年$\frac{哥}{弟}=\frac{3}{1}$,则年龄差是2的倍数;则年龄差是4、3、2的倍数,则只有A.12选项符合,选它。
2、对余数型补充一个题:
例1:(坑题)
(2021广东)某学校组织学生外出学农。如果每间宿舍住6名学生,就会缺7张床位;如果每间宿舍住8名学生,就会空出3张床位。则这批学生共有多少人?
A.50 B.45 C.43 D.37
这个题选什么?
选D。这题求的是人,但题目给的信息是床位的数量,因此要转换为人数。缺7张床位意味着多7个人,空3张床位意味着少3个人。
则说明每间宿舍住6人,就会多出来7人;每间宿舍住8人,就会少3人。
则选D成立。
3、补充一个比例型的例题:
(2020天津选调)赵英读一本小说,第一天读了全书的$\frac{4}{7}$,第二天又读了余下的$\frac{3}{5}$,这时还有42页没有读完,这本小说共多少页?
A. 245 B. 255 C. 265 D. 275
这个题选什么?
选A。书的总页数一定是7的倍数,则只能选A了。没想到就这样选出来了!!!4、对于例2(P195),根据资料分析学的线段法也可以进行计算:
则去年B多生产15%,则去年为$4\times(1+15\%)=4.6$
线段法用于什么时候?用于比较现期和基期的时候,有增长率,求现期量或者基期量
5、例3(P195)怎么写呢?
已知今年共录取231个硕士研究生,其中推荐录取的人数比去年减少$\frac{1}{6}$,考试录取的人数比去年增加
$\frac{31}{150}$,则$\frac{今年推荐}{去年推荐}=1-\frac{1}{6}=\frac{5}{6}$,$\frac{今年考试}{去年考试}=1+\frac{31}{150}=\frac{181}{150}$,则今年推荐是5的倍数,今年考试是181的倍数,代入A.今年推荐40人,则今年考试人数为231-40=191,不是181的倍数;代入C.今年推荐50人,则今年考试231-50=181人,是181的倍数,则选C
6、例4怎么写?
$\frac{去西部}{总人数}=96\%=\frac{96}{100}=\frac{24}{25}$,由于总人数为70多人,则由于总人数是25的倍数,则总人数为75人。去偏远中小学为$75\times20\%=15$,大学生村官为15+2=17人,西部参军为15-1=14人。因为$\frac{去西部}{总人数}=\frac{24}{25}$,则去西部的总人数为72,则去国有企业西部为72-15-17-14=26人,选C
7、出一题,是博客1“题型”中“比例型”的“比例型做题思路总结”的“情况5”的解题思路对应的题:
【拓展5】甲乙丙丁四个人一起去踏青,
甲带的钱是另外三个人总和的一半,
乙带的钱是另外三个人的$\frac{1}{3}$,
丙带的钱是另外三个人的$\frac{1}{4}$,
丁带了91元,他们一共带了多少元?
A. 364
B. 380
C. 420
D. 495
这个题选什么?
选C。甲/另=1/2,则总人数是3的倍数;乙/另=1/3,则总人数是4的倍数;丙/另=1/4,则总人数是5的倍数。由于3、4、5互质,则总人数是3*4*5=60的倍数,则只能选C。
8、出一题,是博客1“题型”中“比例型”的“比例型做题思路总结”的“情况6”的解题思路对应的题:
(2021重庆选调)不到30岁的哥哥今年的年龄正好是弟弟年龄的5倍,若干年后哥哥的年龄就是弟弟的4倍,又过了若干年,哥哥的年龄将是弟弟的3倍,则今年两兄弟的年龄差是多少岁?
A. 12
B. 13
C. 14
D. 15
这个题选什么?
选A。今年哥/弟=5/1,则年龄差是4的倍数;若干年哥/弟=4/1,则年龄差是3的倍数;又过若干年哥/弟=3/1,则年龄差是2的倍数;则年龄差是4、3、2的倍数,则只有A.12选项符合,选它。5 方程法
1、如何设置谁为未知数$x$呢?
①设小不设大(避免分数)。如乙是甲的3倍,那就设甲为$x$,这样乙为$3x$,如果设甲为$x$,就出现乙是$\frac{1}{3}x$这个分数了,不行。
②设中间量(方便列式)。主体太多,则从中间量入手。如例1(P196)设置与四个小组相关的量为$x$,即设置四个小组人数相等时候的人数为$x$。
③求谁设谁(避免陷阱)
④出现比例:设份数。如$\frac{甲}{乙}=\frac{5}{3}$,则设一份为$x$,则甲为$5x$,乙为$3x$
2、扩展:不定方程问题
$\bigstar$出现$ax+by=M$、等,为不定方程问题
$\bigstar$方法:分析奇数偶数、尾数、倍数等数字特性,结合选项代入排除
(1)分析奇偶性。如$3x+4y=25$,发现$4y$一定是偶数,因为25是奇数,则$3x$一定是奇数,则$x$一定是奇数。
(2)分析尾数。$ax+by=M$,当$a$或$b$尾数是0或5的时候,考虑尾数。
如$37x+20y=271$,则$x=?$
A. 1 B. 3 C.2 D.4
由于$20y$的尾数一定是0,则由于271,$37x$的尾数一定是1,则选B,只有B的3能让$37x$的尾数为1
(3)分析倍数特性。$ax+by=M$,当$a$或$b$与$M$有公因子时,考虑倍数特性。注意,要找一个最大的公因子!
如$7x+3y=60$,则$x$为多少?(x、y均为正整数)
A. 5 B. 6 C. 7 D. 8
由于$3y$的3是60的公因子,因此$x$得是3的倍数,因此选B.6。为什么能这么做题呢?
因为$7x=60-3y=3(20-y)$,则$7x$为3的倍数。因为7不是3的倍数,因此$x$得是3的倍数才行,这样只能选B.6了
(4)若以上只能排除4个选项的其中2个选项,排除不了剩余2个选项中的其中一个,怎么办?
那就代入求值。例如例4(P197)。
3、补充一个关于”方法“里的”尾数“这个解题思路对应的题:
(2023河北)如果四个连续的正整数之积是个位为4的四位数,则这四个数中最小的是?
A. 6 B. 9 C. 5 D. 10
这个题选什么?
选A。由于5会让乘积后的数尾数为0或5,10会让乘积后的数尾数为0,因此排除CD。由于是4个连续的正整数,为9、10、11、12,因为出现10,因此乘积的个位为0,排除。只能选A。
4、例4只能用尾数排除4个选项的其中2个选项,怎么办?
$10x+5y+z=89$,因为$10x$的尾数为0,$5y$的尾数可以为0或5,则当$5y$的尾数为0时,$z$的尾数为9;当$5y$的尾数为5时,$z$的尾数为4,则选AB。
怎么选出正确选项。只能代入了。由于这个题方程有2个,为:
代入$z=14$,则方程变为:
方程(1)-方程(2),可得$x=-1$,则$z=14$排除。选B
6 工程问题
1、工程问题的公式:总量=效率$\times$时间
如1小时做60题,效率是60题/h
6.1 题型1:给完工时间型(重点)
1、关于题型1
$\bigstar$题型识别:题中有多个完工时间,则是给完工时间题型
$\bigstar$【引例】搬完一车砖,小帅需要2小时,小美需要3小时,现俩人合作,需要多久?
以往的思维都是设置总量为单位1,则小帅的效率是$\frac{1}{2}$,小美的效率是$\frac{1}{3}$,则总效率为$\frac{1}{2}+\frac{1}{3}=\frac{5}{6}$,则总时间为$1\div \frac{5}{6}=\frac{6}{5}$
这样计算有个缺陷,就是要是时间是那种47、36等数字,计算总效率就异常艰难,那怎么办呢?那就使用以下方法
$\bigstar$方法:
(1)方法1:
流程1:赋总量(完工时间的公倍数,如2和3的公倍数是6)
流程2:算效率:计算各自的效率(效率=总量$\div$时间),再计算总效率
流程3:根据工作过程列式计算
(2)方法2:
代入法,如例3(P199)可以用代入法更快
$\bigstar$补充:求最小公倍数
使用短除法
例如:10和25和40
将最外边的数一乘,即$5\times2\times1\times5\times4=200$,即200是最小公倍数
$\bigstar$题目怎么出?
(1)给甲、乙单独完成工程总量的时间,如例1(P198)
(2)给甲单独完成工程总量的时间;给甲、乙合作完成工程总量的时间,如例2(P198)
(3)给其他条件
2、对于例2,怎么写呢?
甲15天做一半,则甲的完工时间为30天;甲乙合作6天做了一半,则甲乙合作的完工时间为12天
30和12的公倍数这里取60。总效率为60/12=5,甲的效率为60/30=2,则乙的效率为5-2=3。则乙的完工时间为60/3=20
3、对于题型1,给一个更难的扩展题:
题1:
(2022福建)一批试卷分配给甲乙两人评。如果甲单独评,需30小时才能完成任务。乙单独评阅,需40小时才能完成任务。现在他们两人一起同时开始评阅,经过25小时评卷结束。评卷期间甲休息了7小时,问乙在评卷期间休息了多少小时?
A. 6 B. 7 C. 8 D. 9
这个题选什么?
选D。设乙休息了x小时。设x>=7,说明甲乙共同工作了25-x小时,然后甲再继续工作x-7小时。
30和40公倍数是120,设总量为120。甲效率为4,乙效率为3,则总效率为7。
则7(25-x)+4(x-7)=120,则解出来x=9,选D。
还能假设x<7,但是因为已经选出x=9了,因此没必要再假设了。
以上是我的解题方法,感觉特别复杂。但其实根本不用这样,可以这么写:
120是30和40的公倍数,则设总量为120。甲效率为120/30=4,乙效率为120/40=3
则设乙工作了T小时,则$(25-7)\times4+3\times T=120$
解出来T=16,则乙休息了25-16=9小时
即直接计算甲、乙分别工作了几个小时,他们的工作量加起来就是总工作量。而不用关注他们共同工作了几小时,因为总效率本来就是甲、乙相加得到的
6.2 题型2:给效率比例型(重点)
1、关于题型2
$\bigstar$题型识别:题目中给效率比例的3种形式中的一种
$\bigstar$【引例】搬一堆砖,甲和乙的效率比为2:1,合作3小时完成。现在,甲先做2小时,然后再交给乙做,问乙需要做多少小时?
解:设甲效率为2,乙效率为1,则总量为(2+1)$\times$3=9。甲做2小时,做了2$\times$2=4;还剩9-4=5,则乙做了5/1=5小时
$\bigstar$方法:
流程1:赋效率(题目会给效率比例,取满足效率比例的效率即可)
流程2:算总量,使用公式效率$\times$时间=总量
流程3:根据题意完成工作
$\bigstar$效率比例的3种形式:
(1)直接给。如甲:乙=3:4
(2)间接给。
① 时间相同,效率和工作量成正比。如甲完成的50%的时间与乙完成25%的时间相同,则效率比为甲:乙=50:25=2:1
② 工作量相同,效率与时间成反比。如甲4天的工作量等于乙3天的工作量,则效率比为甲:乙=3:4
③ 给具体人数或机器数。如题目给50个人修路、30台机器收割麦子等信息,则50个人之间/30台机器的效率肯定是相同的,则赋值每个人/每台机器的效率为1
6.3 题型3:给具体单位型(简单)
1、关于题型3
$\bigstar$题型识别:题目给出具体效率、具体工程量
$\bigstar$【引例】老邓有120栋楼要收租,11月他想休息10天,那么11月剩下的时间平均每天需要收多少栋楼的房租?
解:都不用列方程求解,直接120/(30-10)=6
$\bigstar$方法:
很简单,直接根据问题设未知数列方程求解
2、对于例7(P199),可以用另一个角度做题。你看对于效率,甲:乙=5:9,则时间上甲:乙=9:5(利用了效率与时间成反比)
则设9x-4=5x+2,则x=1.5,则丙时间为5$\times$1.5+2=9.5h,然后就可以求丙的效率
7 经济利润问题
7.1 基础经济
1、关于基础经济
$\bigstar$基础经济公式:(进价即成本)
(1)利润=售价-进价
(2)利润率=利润$\div$进价
(3)售价=进价$\times$(1+利润率)
$\bigstar$概念辨析:
(1)折扣:打N折就用原价乘以0.N,如八折是80%的折扣
(2)定价、进价,不是一个东西
(3)售价和定价不是一个东西,可能定价$\times$折扣=售价,有可能定价=售价
$\bigstar$扩展:
(1)由于利润=售价-进价,则因为进价肯定不会变,则售价的变化=利润的变化。如进价为100,我一开始售价以200卖,则利润为200-100=100;我后来给售价200打折卖,打八折,则售价为200$\times$0.8=160,则此时利润为160-100=60。利润的变化是100-60=40,而售价的变化是200-160=40,则确实售价的变化=利润的变化
(2)总利润=单件利润$\times$销量
(3)总收入=售价$\times$销量
$\bigstar$方法:
(1)方程法:题干给出价格、数量等具体值设未知数,套公式列方程求解
(2)赋值法:题干未给出价格、数量等具体值,往往赋进价(100),利用公式直接计算。如例3(P201)
补充:当条件太多、关系太乱时,可列表格梳理
2、对于例1(P200),除了一开始我用的那种方法(列二元一次方程求解),还可以用“售价的变化=利润的变化”这个关系,则100-70=0.095$\times$定价-0.09$\times$定价,则定价为600;利润=售价-进价,则进价=0.09$\times$600-70=470,则选B
7.2 分段计费
1、关于分段计费
$\bigstar$出题背景:在生活中,税费、水电费、停车费等,有多段计费标准
$\bigstar$计算方法:
(1)按标准分开计算
(2)代入法
$\bigstar$【引例】某地出租车收费标准为:3公里内起步价8元;超出3公里的部分,每公里2元。小明打车坐了12公里,共花费多少钱?
解:8+(12-3)$\times$2=26元
7.3 函数最值
1、关于函数最值
$\bigstar$出题背景:在生活中,贵的东西就卖的少,便宜的东西就卖的多
$\bigstar$题型特征:价格和销量此消彼长(即价格下降,销量就上涨;价格上涨,销量就下降),问如何定价总收入/总利润最高?
$\bigstar$【引例】售价为3000元时,可卖出16万件。若售价每提升300元,销量会降低1万件。请问当售价定为多少元时,总收入最高?
我一开始设售价为$x$,则式子为$(16-\frac{x-3000}{300}\times1)x$,这样会有分母,很难计算。而老师的方法更简单,为:
设提升了$x$次300元,则式子变为$y=(3000+300x)(16-x)$,而且不是用化为式子$ax^2+bx+c$进行计算,而是将$y=0$进行计算,得出$x_1=-10$和$x_2=16$,则最终最值处的$x=\frac{x_1+x_2}{2}=\frac{-10+16}{2}=3$,则售价为$3000+3\times300=3900$元
$\bigstar$计算方法:
通过引例,我们可以得到计算方法为:
设提价次数为$x$次,写出式子$y=(ax+b)(cx+d)$,
令$y=0$,解得$x_1$和$x_2$;
当$x=\frac{x_1+x_2}{2}$时,取得最值
$\bigstar$补充:一元二次方程求根公式
对于$ax^2+bx+c=0$,其求根公式为$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$
$\bigstar$注意点:
(1)总收入最大$\neq$总利润最大
2、$\bigstar\bigstar\bigstar$对于例2(P202),我的思路是,列出式子$(10+x-8)(100-10x)\geq350$,然后解方程,但是这样很麻烦!
而老师说,根本没必要这样,而是求式子$(10+x-8)(100-10x)$的最大值对应的$x$即可,因为此时的最大值(即最大利润)肯定大于350元
让$(10+x-8)(100-10x)=0$,则求出$x_1=-2$与$x_2=10$,则最大值对应的$x=\frac{-2+10}{2}=4$,即售价为$10+4=14$元,此时对应选项B,是13元和15元之间的数
8 行程问题
1、关于行程问题
$\bigstar$公式:路程=速度$\times$时间
注意:对于猜选项,要是想选出路程,假设时间固定为18h,则路程一定是18的倍数(根据第一章的倍数特性法),因为国考省考题大多出速度是整数的题
$\bigstar$考察题型:
(1)普通行程(简单)
(2)相对行程(重点)
$\bigstar$补充知识:
(1)匀加速、匀减速(热门考点!!!)
假设一辆车从速度0匀加速到速度60,行驶了2h,则它经过的路程是多少?
对于匀加速、匀减速,路程$S=v_{平均}\times T$,$v_{平均}=\frac{v_初+v_末}{2}$,则路程$S=\frac{0+60}{2}\times2=60$
扩展:若一辆车从0开始匀加速到最大速度,然后从最大速度匀减速到0,则这一段路程的平均速度是多少?
匀加速时候的平均速度是$v_{平1}=\frac{v_初+v_末}{2}=\frac{0+v_大}{2}=\frac{v_大}{2}$,匀减速时候的平均速度是$v_{平2}=\frac{v_初+v_末}{2}=\frac{v_大+0}{2}=\frac{v_大}{2}$,因为匀加速路段的平均速度等于匀减速路段的平均速度,则就可以断定整段路程的平均速度为$\frac{v_大}{2}$
8.1 相对行程问题(重点)
1、关于相对行程问题
$\bigstar$情况1:直线相遇
同时相向而行,都是匀速,且在时间$T_遇=T$的时候相遇,如下图情况: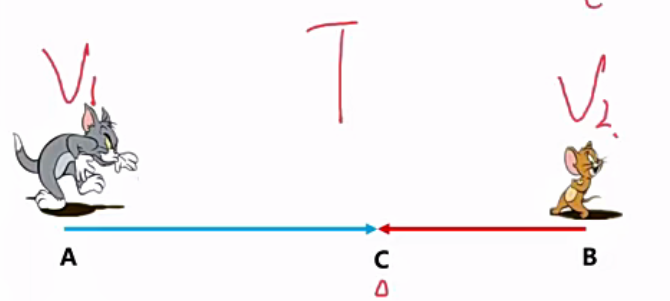
公式推导:$S=v_1\times T_遇+v_2\times T_遇=(v_1+v_2)\times T_遇=v_合\times T_遇$,即$S=v_合\times T_遇$
$\bigstar$情况2:直线追及
同时同向而行,都是匀速,设$S_差$是追及刚开始时两人相差的距离(即A的起点和B的起点的距离),$T_追=T$是A追上B的时间,且A的速度>B的速度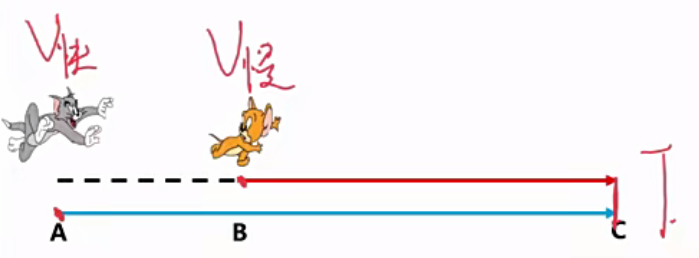
公式推导:$S_差=S_猫-S_鼠=v_快\times T-v_慢\times T=(v_快-v_慢)\times T=v_差\times T$,即$S_差=v_差\times T$
注意,$S_差$是速度不一样的那个时刻的距离差,一定要注意这个哦!!!
$\bigstar$情况3:环形相遇
(1)同时同点反向出发,即A和B从同一个点出发,A顺时针走,B逆时针走,在圆上同一个点相遇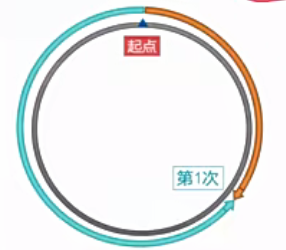
每相遇一次,A和B的路程合起来是一圈;相遇N次,$S_和=N圈$
且公式为$S_和=v_和\times T_遇$
(2)如果不是同一个点出发呢?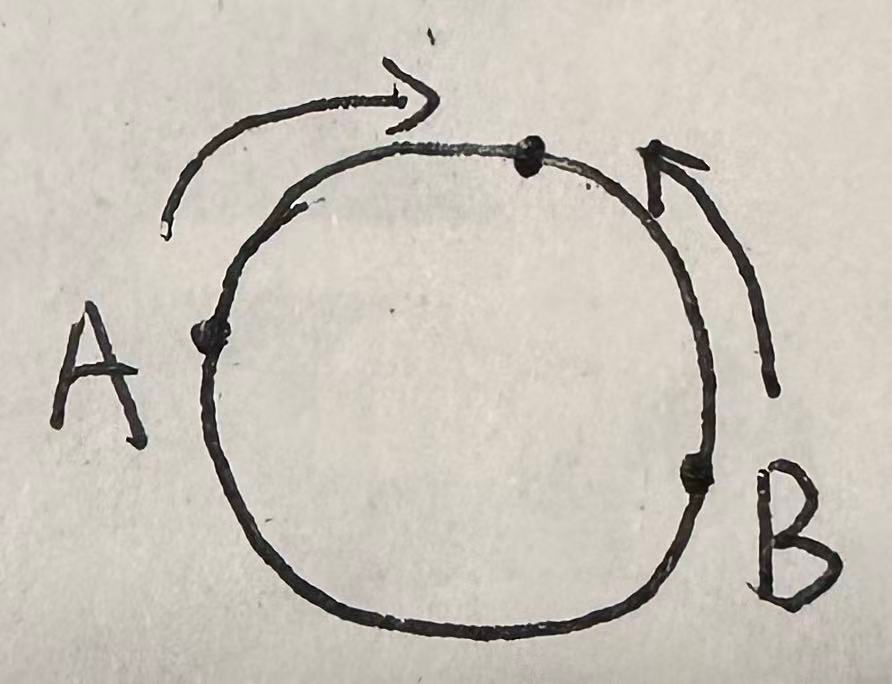
第一次相遇就是正常套公式计算;后续相遇就是同点出发套公式
$\bigstar$情况4:环形追及
(1)同时同点同向出发,A的速度大于B的速度
每追上1次,多走1圈;追上N次,$S_差=N圈$
公式:$S_差=v_差\times T_追$
(2)那如果不是同一点出发的呢?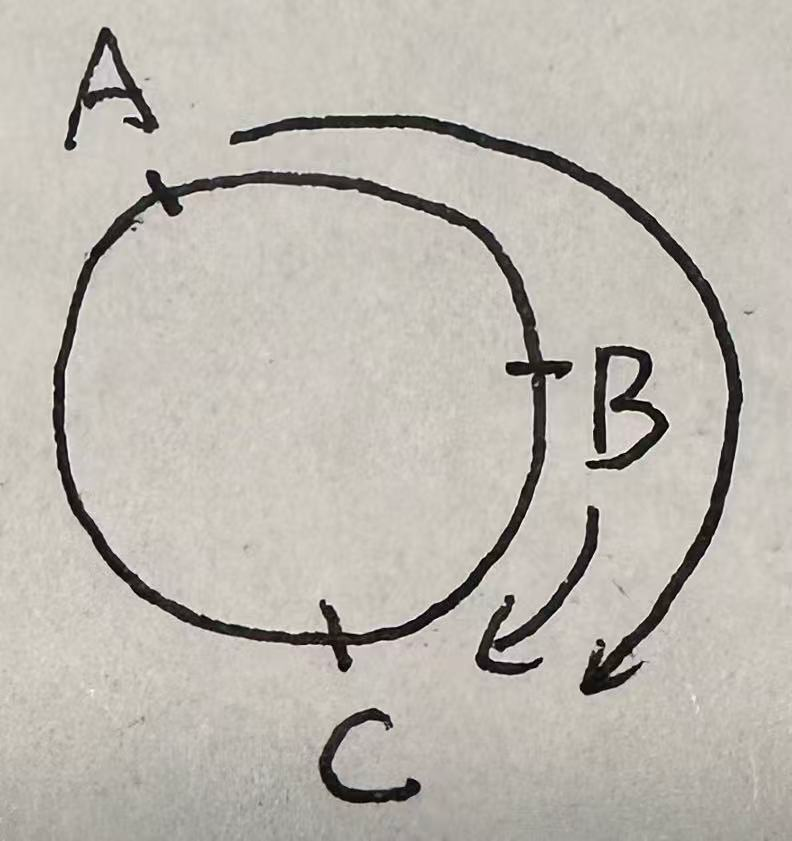
第一次追及就是正常套公式计算;后续追及就是同点出发套结论
$\bigstar$补充方法:比例法
用题来讲解比例法:
【拓展3】甲乙两人在一条400米的环形跑道上同点同时出发,同向匀速跑步。当甲第三次追上乙的时候,乙跑了2000米。问甲的速度是乙的多少倍?
A. 1.2 B. 1.5 C. 1.6 D. 2.0
解:第三次追上,则$S_差=3\times400=1200$,乙跑了2000米,则甲跑了$S_乙+S_差=2000+1200=3200米$。因为时间T相同,则$\frac{S_甲}{S_乙}=\frac{v_甲}{v_乙}$,即$\frac{v_甲}{v_乙}=\frac{3200}{2000}=1.6$,选C。
2、给一个容易多想的坑题:(关于“情况1:直线相遇”的题)
【拓展2】甲乙两人在相距1200米的直线道路上相向而行,一条狗与甲同时出发跑向乙,遇到乙后立即调头跑向甲,遇到甲后再跑向乙,如此反复,已知甲的速度为40米/分钟,乙为60米/分钟,狗为80米/分钟。不考虑狗调头所耗时间,当甲乙相距100米时狗跑了多少米?
A. 1100 B. 1000 C. 960 D. 880
这个题选什么?
选D。甲乙相距100米的时候,经过了(1200-100)/(40+60)=11分钟,则狗跑了11*80=880米,选D。一开始肯定容易多想,想算狗遇到乙、甲几次,各跑了多少米,但是这没必要想。因为题目暗示我们狗是不停地跑的,因此甲乙运行11分钟,狗也运行11分钟(这是不被影响的!!!),因为匀速就可以根据公式路程=速度*时间写出来狗跑了多少米。
3、对于例4(P204):
(1)例4(P204)一定要写!!!是热门的模板题!!!两个人走到一个地点,然后一个人忘了什么东西回去了,另一个人还在走,那个回去的人回去后为了追另一个人,速度变快
(2)以及,对于例4(P204),我忽略了,小王回甲地那段时间,小李还在走!!!一定要记住!!!
因此写成$\frac{1}{4}v+(\frac{1}{4}+x)v=15$,而不是$\frac{1}{4}v+xv=15$
(3)例4的方法2:(老师的方法,你也要会!!!)
小王回去甲地后,从甲地出发,它的速度才变成1.2v(设原来速度为v),这时候才有速度差,此时小王和小李的距离差为$\frac{1}{4}v+\frac{1}{4}v=\frac{1}{2}v$(因为小王回去的时候,小李也还在走),设相遇时间为T,则根据公式$S_差=v_差\times T$,则$\frac{1}{2}v=(1.2v-v)T$,则T=2.5h,小李总共走了$\frac{1}{4}+\frac{1}{4}+2.5=3$小时,则小李速度为$\frac{15}{3}=5km/h$
4、对“情况4:环形追及的不是同点出发”补充一个习题:
【拓展4】甲乙两人在一条400米的环形跑道上从相距200米的位置同时出发,同向匀速跑步。当甲第三次追上乙的时候,乙跑了2000米。问甲的速度是乙的多少倍?
A. 1.2 B. 1.5 C. 1.6 D. 2.0
这个题选什么?
选B。第一次相遇,S差=200米,第二次第三次相遇,S差=400*2=800米,则S差和=200+800=1000。S甲=S乙+S差=3000米,则v甲/v乙=S甲/S乙=3000/2000=1.5,则选B。9 几何问题
1、考场思维:
(1)几何配图,则结合图选出选项。如例1(P205),从图中可以大致看出,花坛的边长大约是路宽的三倍,则边长为3,选B
2、需要记忆的公式:
圆柱体体积公式:$\pi r^2h$
圆锥体体积公式:$\frac{1}{3}\pi r^2h$
梯形面积公式:$\frac{(上底+下底)\times h}{2}$
密度公式:$\frac{m}{V}$,即$\frac{质量}{体积}$
3、常见题型考察:
(1)题型1:将一个物体放入水中淹没是最常见对体积的考查。该物体的体积等于水面上升部分的体积
【拓展4】一个长方体实心零件,长、宽、高分别为12厘米、8厘米和4厘米。如将其最大面朝下放在另一个长方体水槽中,零件将被完全淹没且水面上升3厘米。问零件最大面的面积比水槽底面积小多少平方厘米?
A. 32 B. 64 C. 96 D. 128
解:长方体体积为$12\times8\times4=384$,水面上升体积=长方体体积,则水槽底面积=$\frac{水面上升体积}{3}=\frac{384}{3}=128$,则零件最大面的面积比水槽底面积小$128-12\times8=32$,选A
9.1 三角形相关
1、三角形相关
$\bigstar$考点1:勾股定理相关
(1)公式:$a^2+b^2=c^2$
(2)常考勾股数:(3,4,5)、(6,8,10)、(5,12,13)
(3)特殊角直角三角形三边关系: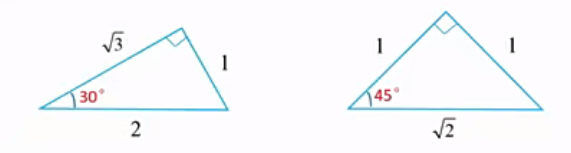
(4)勾股定理的题的补充方法:
① 对比选项求出(感觉常用!!!),不用计算根号。看例3(P206),设B、C两点之间的距离为S,画图最后可知$(\frac{4}{3}S)^2=30^2+S^2$,则$30^2=\frac{7}{9}S^2$,要计算$S=\sqrt{900\times\frac{9}{7}}$,这也太难算了。但是老师教了一种不用计算根号的方法!因为B、C距离平方为$S^2$,且$S^2>\frac{7}{9}S^2$,则由于得出$30^2=\frac{7}{9}S^2$,可以得出$S^2>30^2$,由$S>0$则$S>30$,直接选D,不用算出根号就可以直接锁定选项!
② 勾股定理不好计算数字,可以用选项代入法!根据常见勾股数,来选择选项代入!!!
(5)补充知识:
① 在圆中,有一个三角形,有一条边是圆的直径,则直径所对的三角形的角度为90度,即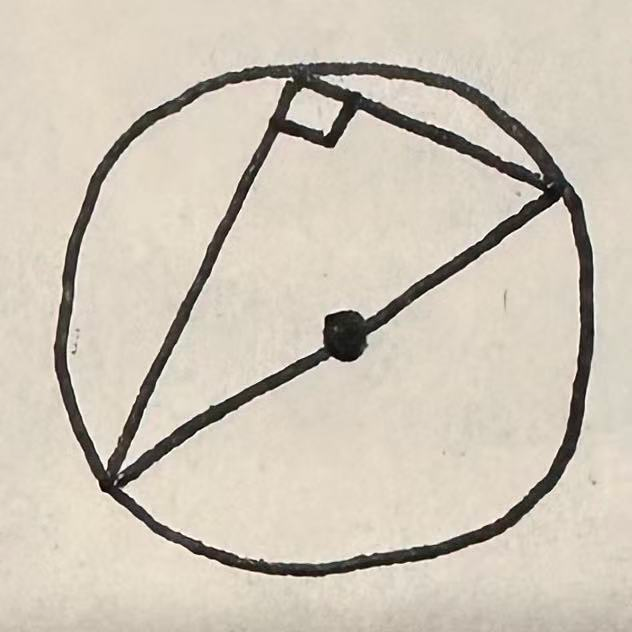
② $\sqrt{3}=1.732$;$\sqrt{2}=1.414$
$\bigstar$考点2:最短路径
(1)考察方式:求AB两点到直线距离之和最短
(2)解题原理:两点之间,直线最短
(3)解题技巧:镜面对称后连线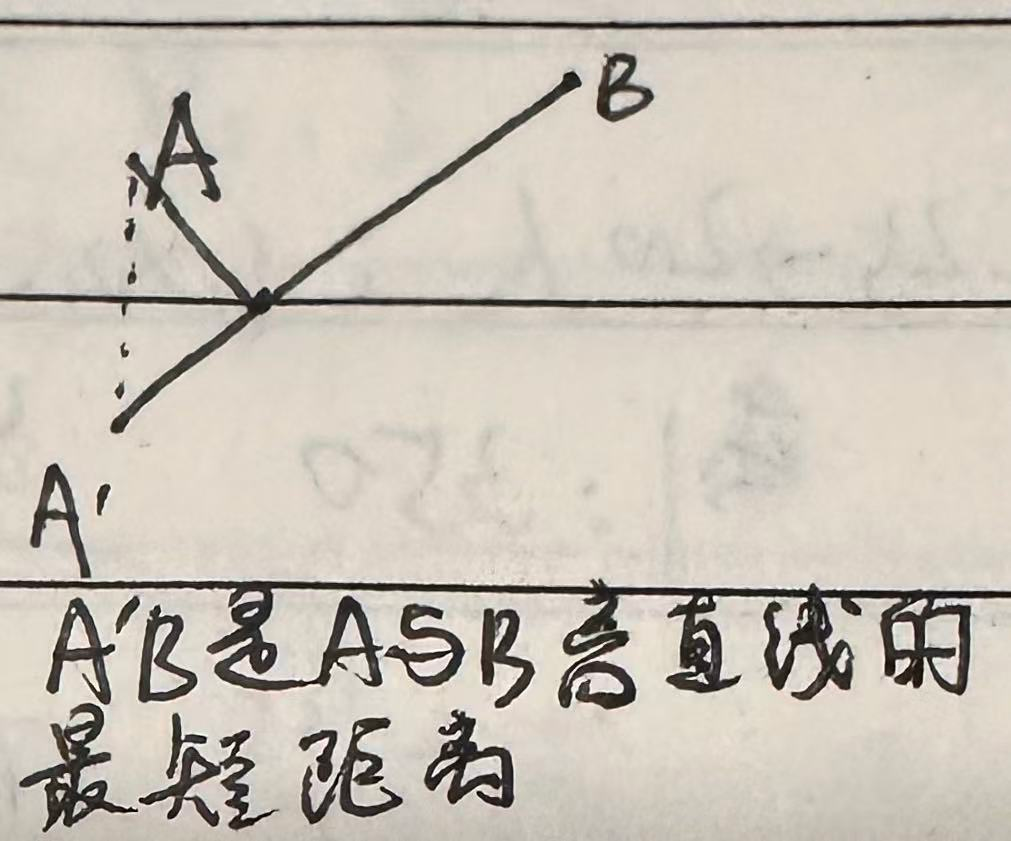
这里是对A镜面对称,换成对B镜面对称也可以!!!
特殊情况:若A点和B点在同一直线上,则A’点与B的连线经过直线的点C是“中心点”,对应点D是在直线AB的中间,即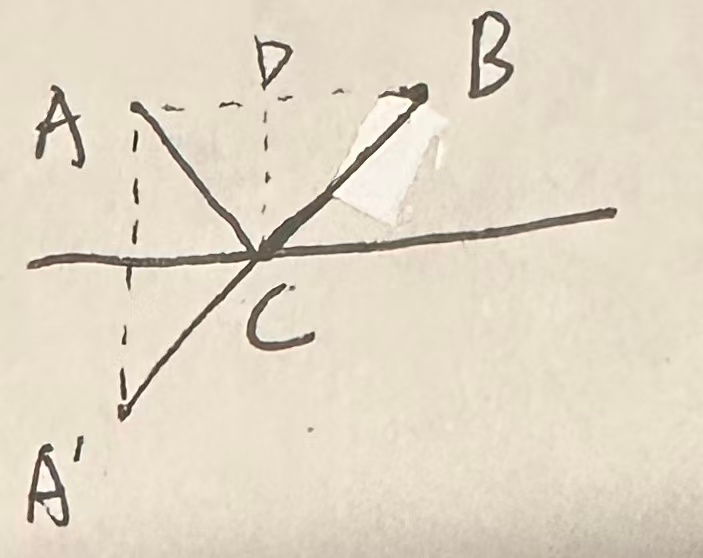
$\bigstar$考点3:面积相关
(1)知识点:
① 面积比转化为高/底之比:

② 通过相似三角形得出面积相关结论: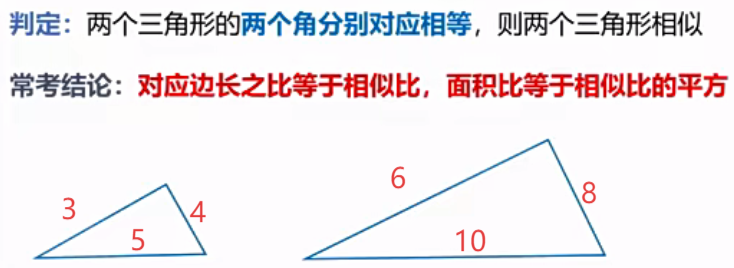
你看大三角形边长和小三角形对应边长的比都是2:1,因此相似比是2:1,面积比是4:1
还能利用全等三角形,如例8(P207)
2、扩展题目:对应“考点3:面积相关”的“知识点②”
【拓展6】演播厅的地面形状是边长为100米的正三角形,现要用边长为2米的正三角形砖铺满(如图所示)。问需要用多少块砖?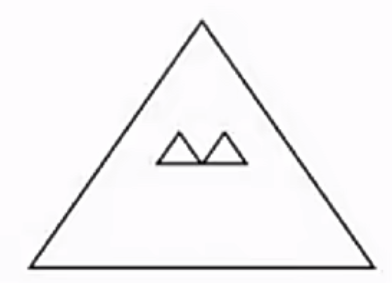
A. 2763 B. 2500 C. 2340 D. 2300
这个题选什么?
选B。相似比是100:2=50:1,则面积比是相似比的平方,为2500:1,则选B。3、例8(P207)的计算方法写在书上了,反正是要计算,有不计算的方法吗?
介绍写这一题的考场思维:
(1)$S_{ABE}=24$,因为AB=AD,对应高三角形ADE比三角形AEB大,则$S_{ADE}>S_{ABE}=24$,且高是略大,则面积也是略大,选32(因为32比24略大)
(2)将AC和BD连线,如下图: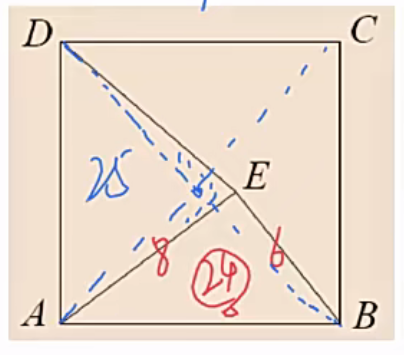
发现$S_{ADE}>\frac{100}{4}=25$,且比25略大,则选32
(3)有一个方法更好:
过E点做AD的垂线,则: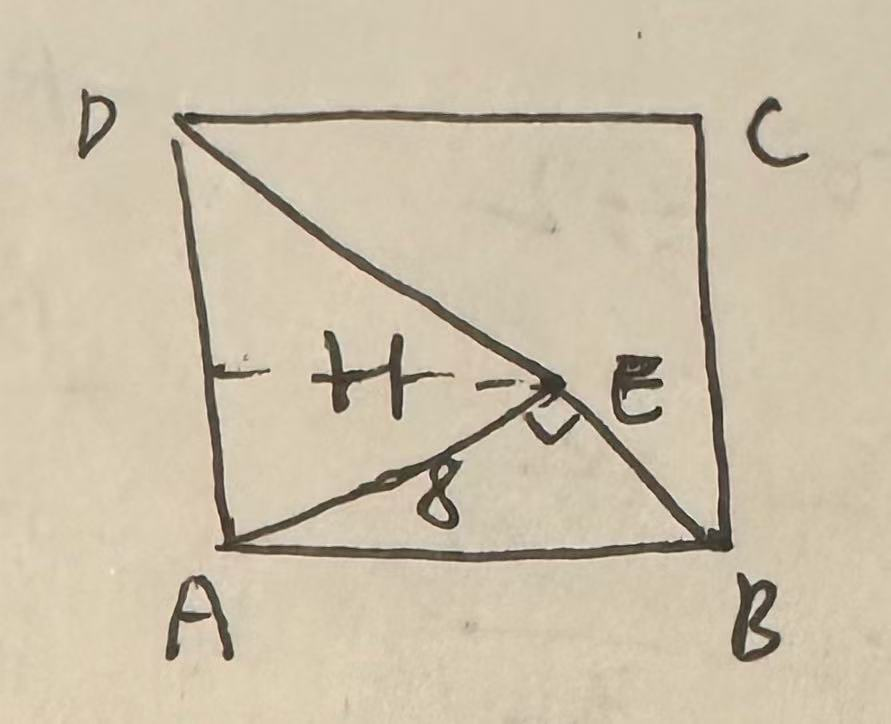
可知$H<AE=8$,则$S_{ADE}=\frac{H\times10}{2}<\frac{8\times10}{2}=40$,同时,$S_{ADE}\gt S_{ABE}=24$(由(1)知道),则只能选32
10 排列组合问题
10.1 基础概念
1、关于排列组合
$\bigstar$基础概念:
(1)分类与分步
分类(相加):要么….要么.…(多者选其一)
分步(相乘):既…又.(都要满足)
判断题目是分类还是分步,就是将“要么….要么.…”或“既…又”代入题目,看是哪个,就能判断是相加还是相乘:
① 如例1(P209),因为荤素是“既…又”的关系,因此是相乘
(2)排列与组合
排列(A):与顺序有关(选完人后需要排序)
组合(C):与顺序无关(只需要选人,不需要排序)
8人中选出3人排成一队照相,共有$A_8^3$种站队方式
8人中选3人打扫卫生,共有$C_8^3$种选取方式
$\bigstar$公式:
$A_n^m=n\times(n-1)\times(n-1)\times…\times(n-m+1)$,$m$个数相乘
$C_n^m=\frac{A_n^m}{A_m^m}=\frac{n\times(n-1)\times(n-2)\times…\times(n-m+1)}{m\times(m-1)\times(m-2)\times…\times1}$
$A_n^1=C^1_n=n$(从n个随便选一个就是n种情况)
$C_n^m=C_n^{n-m}$(10个里面挑8个等价于10个挑2个;什么意思呢?就是例如100个里面选98个太麻烦了,不如100个里面选2个不要的,因此100个里面选98个相当于100个里面选2个)
2、对于例2(P210),我有话要说。
方法1:我是在正面的角度考虑,进行分类讨论
方法2:老师说还能从反面的角度考虑,反面就是只有男/只有女。只有男,就是$C_6^3=20$,只有女,就是$C_3^3=1$,总方案数是$C_9^3=84$,则此题为84-20-1=63
方法3:男女各选一个,剩下1个人在剩下7人里面随便选一个。这样可以吗?
不行!!!因为有可能男女各选一个的时候,选的是男1、女1,然后剩下7人里随便选一个,选的是男2;还有可能男女各选一个的时候,选的是男2、女1,然后剩下7人里随便选一个,选的是男1。这样就出现了重复的选择。因此这种方法不行!!!($\bigstar$感觉得把这种方法记住,然后写其他题的时候注意不要犯这个错误)
10.2 经典题型
1、方法1:凑数字,即枚举法
$\bigstar$题目特征:凑钱数;情况数很少(10以内,选项的数字都是10以内)
$\bigstar$【引例】妈妈给了小明8块钱让其去买早餐并且把钱用完。早餐摊只有两种食品,包子3块钱一个,馒头2块钱一个,问小明有( )种不同的买法?
解:3+3+2、2+2+2+2。即2种买法
$\bigstar$思路:从数字最大的开始枚举
2、方法2:相邻问题,即用捆绑法
$\bigstar$题目特征:必须相邻(在一起)
$\bigstar$【引例】A、B、C、D、E五个人站成一排照相,其中A、B是一对情侣,要求照相时必须相邻,一共有多少种排法?
解:先捆,考虑小情侣内部顺序,即$A_2^2=2$,把捆绑后的看成一个主体,即看成4人排列,即$A_4^4=24$,则为$A_2^2\times A^4_4=48$种
$\bigstar$思路:
先捆:把要相邻的主体捆绑起来,考虑内部顺序;
再排:将捆绑后的看成一个主体,和剩下的主体一起排列。
3、方法3:不相邻问题,即用插空法
$\bigstar$特征:不能相邻(不在一起)
$\bigstar$【引例】A、B、C、D、E、F、G七个人站成一排照相,其中A、B、C闹矛盾要求照相时都不能相邻,一共有多少种排法?
解:D、E、F、G随便排列,即$A_4^4=24$,将A、B、C对D、E、F、G进行插空,D、E、F、G有5个空,即$A_5^3$,则最后有$A_4^4\times A_5^3=1440$
$\bigstar$思路:
先排:先安排可以相邻的主体,形成若干个空位;
再插:将不相邻的主体插入到空位中。
4、方法4:同素分堆问题,即用隔板法
$\bigstar$【引例】7个相同的苹果分给三个小朋友,每人至少分一个,有多少种分法?
解:7个苹果,往七个苹果中间(6个空位)放入2个板子,就可以将苹果分成3堆。则是$C_6^2=\frac{6\times5}{2\times1}=30$
$\bigstar$题目特征:n个相同的东西分给m个人,每人至少一个
$\bigstar$方法:$C_{n-1}^{m-1}$
5、对隔板法进行补充:
(1)【拓展4 变形】有25颗苹果,打算全部分发给A、B、C三人若每人至少拿到6颗苹果,则有多少种分发方式?
A. 15 B. 20 C. 35 D. 36
$\bigstar$方法:需要n个,先给n-1个就变成还需要至少一个,然后再套公式
给三个人每人各5颗苹果,则$25-3\times5=10$,则最后为$C_9^2=\frac{9\times8}{2\times1}=36$
(2)【拓展5 变形】物业派出小王、小曾、小郭三名工作人员负责修剪小区内的6棵树,每名工作人员至少修剪1棵,若希望小王至少修剪3棵,则修剪棵数的分发方式有几种?
解:
方法1:正面求解。小王至少修剪3棵,则小王修剪3棵、4棵。小王修剪3棵时,还剩3棵,中间放1个隔板,则为$C_2^1=2$;小王修剪4棵时,还剩2棵,中间放1个隔板,即$C_1^1=1$。则方式共1+2=3种
方法2:反面求解。小王至少修剪3棵的反面是小王只修剪1棵或只修剪2棵。小王修剪1棵,还剩5棵树,中间放一个隔板,即$C_4^1=4$;小王修剪2棵,还剩4棵,中间放1个隔板,即$C_3^1=3$。则方式共10-(4+3)=3种
11 概率问题
1、情况1:给情况(个数)求概率
$\bigstar$公式:$概率=\frac{满足要求的情况数}{所有情况数}$
$\bigstar$【引例】全班100人,男生40人。随机挑选2人全部都是男生的概率?
解:$\frac{C_{40}^2}{C_{100}^2}=\frac{40\times39}{100\times99}$
2、情况2:给概率求概率
$\bigstar$方法:
(1)分类用加法:$P=P_1+P_2+…+P_n$
(2)分步用乘法:$P=P_1\times P_2\times … \times P_n$
$\bigstar$举例:
【引例1】老邓随机购买一张彩票,中一等奖概率为10%,中二等奖概率为20%,中三等奖概率为30%,问这张彩票中奖的概率是多少?
解:要么中一等奖、要么中二等奖、要么中三等奖,即分类相加,即10%+20%+30%=60%
【引例2】买完彩票后老邓又去刮刮乐,刮中100万的概率为50%,问老邓今天既彩票中奖又刮刮乐中奖的概率为多少?
解:既彩票中奖又刮刮乐中奖,即分步相乘,即60%$\times$50%=30%
3、对于例2(P211),我有话要说。这种“至少”的题,用反面来写最好!这一题的反面就是叶雕和皮影展厅一个都没被选中,这个很好求!
或者选项里有加和为1的情况,用反面来做可能更好做!例2就是选项A和C加和为1
4、补充题目:
【拓展5】中秋节前夕,小赵买了6个外观相同的月饼,其中有3个是蛋黄馅的。回到家后,小赵从中任取3个月饼,里面恰好有1个是蛋黄馅的概率是:
A.9/20
B.1/2
C.3/5
D.11/20
这个题选什么?
选A。即从3个蛋黄馅月饼里挑1个,从剩下不是蛋黄馅的月饼里挑2个,即C_3^1*C_3^2=9种,总情况数为C_6^3=20,则是9/20,选A。5、对于例4(P212),我犯了一个致命的错误!我知道要么第一、二批中奖,要么第一、三批中奖,要么第二、三批中奖,然后我就写成了$0.6\times0.2+0.2\times0.2+0.6\times0.2=0.28$,然后不知道选哪个
以上是错的,因为张先生三次都参与了,因此在第一、二批中奖的时候,还要算上第三批未中奖的概率,即要写为$0.6\times0.2\times0.8+0.2\times0.2\times0.4+0.6\times0.2\times0.8=0.208$,选A
12 容斥原理问题
1、关于容斥原理问题:
$\bigstar$容斥原理本质:多个集合有交叉,去重补漏
$\bigstar$考查类型:
(1)两集合容斥原理
① 两集合容斥原理的方程:$A+B-A\cap B=$总数-都不,等号左右两边两式相等,构成一个方程,能求东西
(2)三集合容斥原理
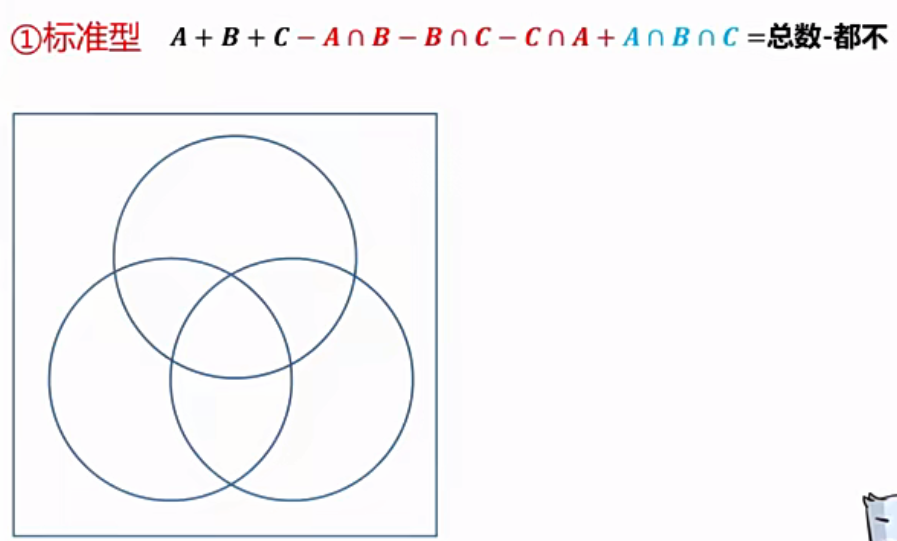
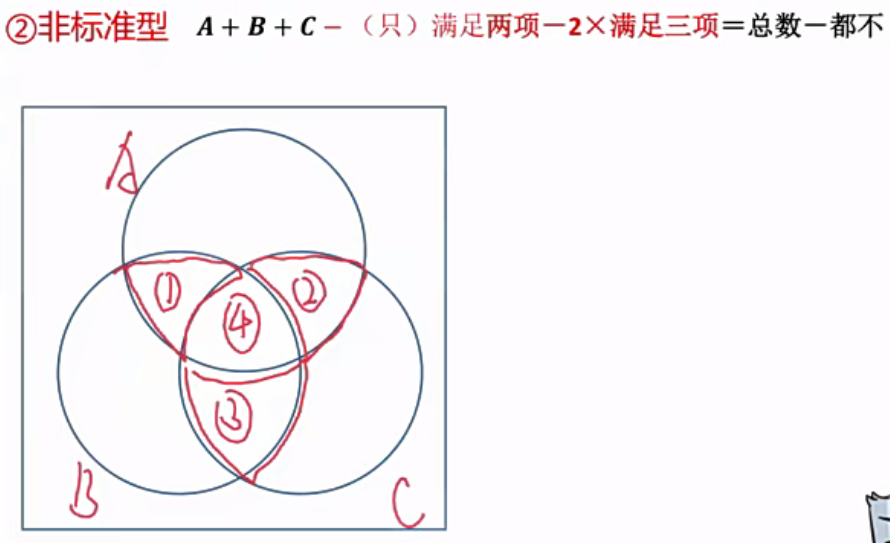
对于以上这个方程,从图中可以解释,即A+B+C-①-②-③-2$\times$④=总数-都不
③标准型和非标准型有什么区别?
图中的①即只有二者,A$\cap$B即二者及以上
如例3,订阅A、B期刊的有57人,其中包含了只订阅A、B期刊的,和订阅了A、B、C期刊的人数,因此是A$\cap$B=57
如例4,申请了其中两类专利的有39家,只包含了申请其中两类专利的,即是①+②+③=39
④列出方程后,挺难计算的,怎么办?用尾数法
$\bigstar$解题方法:
(1)列方程法
列出二集合容斥原理和三集合容斥原理的方程,使用尾数法计算
(2)画图法
用不了方程,就用画图法,如例5(P213)
$\bigstar$补充关系:
(1)$A\cap B\leq[A,B]_{min}$,如例1(P212),可知$A\cap B\leq[A,B]_{min}=[40,46]_{min}=40$
2、对于例2(P213),我有话要说
给数值范围和比例关系,没给具体值,但问具体值,一般都是考倍数特性法,通过倍数关系确定具体值
这题也是一样,物理、化学均不及格的人数占全班的14%,$14\%=\frac{7}{50}$,因此全班人数是50的倍数,又因为全班人数不超过70人,因为$\frac{物化不及格的人数}{全班人数}=\frac{7}{50}$,因此全班人数只能是50人。则物化不及格的人数为7人。化学及格人数为50$\times$60%=30,物理及格人数为30+10=40,则式子为30+40-$A\cap B$=50-7,则$A\cap B=$27
3、对于例3(P213),我有话要说
这个题的方程是$125+126+135-57-73-x+31=240-17$,这个方程要计算出x很复杂。看选项每个数字的尾数都不一样,因此此题计算x可以用尾数法,而不是直接计算,比直接计算快多了!!!
4、【拓展】某班参加学科竞赛人数40人,其中参加数学竞赛的有22人,参加物理竞赛的有27人,参加化学竟赛的有25人,只参加两科竞赛的有24人,参加三科竟赛的有多少人?
A. 2 B. 3 C. 5 D. 7