资料分析
1 前提小技巧
1、$14\% \approx \frac{1}{7}$
2 速算技巧
2.1 截位直除
1、算除法的方法：
（1）先学怎么保留有效数字：就是简单的四舍五入
从左起第一个不是0的数开始，保留几位画几位，看下一位上的数字，四舍五入：
1.4508 保留2位:15 1.4508 保留3位:145 直接把小数点丢掉
42462 保留2位:42
1.125 保留 2 位:11 1.125 保留3位
0.14 保留2位:14（这个肯定要知道！）
（2）再学保留几位有效数字：
$\bigstar$看选项差距:
差距大，保留2位，算的快，还能算得准
差距小，保留3位，算的慢些，但保证准
$\bigstar$差距大：首位数字都不一样 → A.25 B.36
首位数字相同，第二位数字差值>首位 → A.13 B.15
$\bigstar$差距小：首位数字都不一样，但临界(即很接近) → A.29 B.30
首位数字相同，第二位数字差值≤首位 → A.207 B.217；又如 A.207 B.227
步骤：先看首位数字相不相同，如果不同则差距大；如果相同，看第二位数字的差值的情况
（3）保留分子还是分母的有效数字呢？
情况1：
注意！分子抄3位，不是分子四舍五入保留3位哦！！！
例如：$\frac{127.38}{1.4508}$，选项差距大，那怎么保留呢？
因为选项差距大，则分母保留2位（保留有效数字的时候要把小数点直接丢掉），则分子抄3位（不是四舍五入），即$\frac{127}{15}$
又如：$\frac{232.8934}{1.125}$，选项差距小，那么怎么计算呢？
因为选项差距小，则分母保留3位，则分子抄4位，即$\frac{2328}{113}$
情况2：
注意！分子、分母保留相同的位数，即分子、分母都要四舍五入，这和一步除法不同，一步除法的分子不用四舍五入，而分母要四舍五入
为什么保留相同的位数？为了分子分母好约分
选项差距大，则分子分母保留2位；选项差距小，则分子分母保留3位
例如$4774\div \frac{2828}{1+10.6\%}$，选项差距大，那怎么计算呢？
因为选项差距大，因此都保留2位有效数字，即$48\div \frac{28}{11}$，后续的步骤是约分，则写成$12\times\frac{11}{7}=\frac{132}{7}$，然后直接计算132除以7是多少，是1.8几
又如$\frac{26352.1}{32161.9}\div\frac{2254.7}{6946.7}$，选项差距大，怎么计算呢？
因为选项差距大，因此都保留2位有效数字，即$\frac{26}{32}\div\frac{23}{69}$
（4）是否需要考虑位数、小数点、百分号？（可能需要，可能不需要）
在除法中，位数、小数点、百分号只会改变结果的位数，不会改变有效数字
如$\frac{127.38}{1.4508}$，写成$\frac{127}{15}$即可，不用写成$\frac{127}{15}\times10$，因为乘不乘10都不影响最后结果的有效数字！
需不需要考虑位数、小数点、百分号，其实是看选项！
你看例4（P151）的选项，即A和C、B和D有有效数字后面有几个0的区分，那就要考虑位数、小数点、百分号，即乘以几个10；注意，由于选项需要区分有效数字后面有几个0，因此这些选项一定差距大！
如果是例3（P151）的选项，根本不需要考虑位数、小数点、百分号
（5）如果最后计算出来的东西选项里没有，则选一个大于它且最接近它的选项；如选项有1.7与1.9，计算出来是1.8几，则选大于它且最接近它的选项，即1.9
2、选项差距大，则保留2位有效数字，则为$\frac{895}{14}$，由于这一题要考虑有效数字后面有几个0，则不能仅仅写为$\frac{895}{14}$，得写成$\frac{895\times10^4}{14\times10^{-2}}$，则等于$60\times10^4$，即选D
3、第一次遇见多步除法的题，那这题多步除法怎么计算呢？由选项知选项差距大，则分子、分母保留相同的2位，即都要四舍五入
即写成$48 \div\frac{28}{11}$，约分后为$12\times\frac{11}{7}=\frac{132}{7}$，然后直接算除法132除以7等于多少，等于1.8几，则选一个大于它的选项，就是1.9
2.2 分数比较
2.2.1 两个分数的比较大小的方法
1、第一种分数：例如$\frac{73.0}{4061.8}$和$\frac{62.5}{4234.9}$比较大小，即$\frac{大}{小}$和$\frac{小}{大}$，则直接可知$\frac{73.0}{4061.8}$更大
2、第二种分数：例如$\frac{2580}{3787}$和$\frac{5770}{7557}$比较大小，即$\frac{小}{小}$和$\frac{大}{大}$，这种怎么比较大小呢？
涉及知识点：“同大同小”的分数怎么比较？
（1）方法1：竖向直除，分母一般保留2位估算范围
位数相同，看有效数字；位数不同，注意位数
例如$\frac{3050}{47203}$和$\frac{3700}{50251}$比较大小，能看出它们的分子、分母位数都相同，即分子都是4位，分母都是5位
位数相同，则看有效数字。把它们的分母都保留2位，即写成$\frac{3050}{47}$和$\frac{3700}{50}$，3050除以47为六十几，而3700除以50为七十几，看有效位数，6小于7，则$\frac{3700}{50251}$更大
（2）方法2：横向倍数，看分子间几倍，看分母间几倍
分子间倍数大，只看分子，分子大，分数大
分母间倍数大，只看分母，分母大，分数小
例如$\frac{37}{24}$和$\frac{12}{9}$，$\frac{37}{24}=\frac{12\times3^{+}}{9\times2^{+}}=\frac{12}{9}\times\frac{3^+}{2^+}$，由于$\frac{3}{2}>1$，则$\frac{37}{24}>\frac{12}{9}$
以上这种方法，如果是很复杂的数字，就没法全部知道分子分母之间的倍数了，这样其实很麻烦
但是我们可以这样，还是例如$\frac{37}{24}$和$\frac{12}{9}$，分子的倍数是3，分母的倍数是2，则只看分子的倍数，分子的倍数大，则分子大的分数大，即$\frac{37}{24}$大
又例如$\frac{24}{37}$和$\frac{9}{12}$，分子的倍数是2，分母的倍数是3，则只看分母的倍数，分母的倍数大，则分母大的分数小，即$\frac{24}{37}$小
2.2.2 四个分数的比较大小的方法
1、方法1：针对四个分数里找最大最小，则
找最大，以分子最大的分数作为参照，与其他分数逐一比较，如果还有分数比分子最大的分数大，则更新参照
找最小，以分子最小的分数作为参照，与其他分数逐一比较，如果还有分数比分子最小的分数小，则更新参照
根据原则$\frac{大}{小}>\frac{小}{大}$来比较分数的大小，这个原则还是很有用的！
2、方法2：估范围（我更爱用这个）
先按分子的大小排序。要是找最大，按分子最大的开始排序；要是找最小，按分大最小的开始排序
竖向直除，分母一般保留 2位估算范围
位数相同，看有效数字；位数不同，注意位数
例如，
$\bigstar$对比位数相同的$\frac{3850}{40007}、\frac{3350}{43852}、\frac{3050}{47203}、\frac{3700}{50251}$的大小？
分母保留2位，则比较$\frac{3850}{40}=9^+、\frac{3350}{44}=7^+、\frac{3050}{47}=6^+、\frac{3700}{50}=7^+$，则很容易对比出大小
$\bigstar$对比位数不同的$\frac{9245}{13.82}、\frac{31379}{74.06}、\frac{441}{2.36}、\frac{3105}{39.08}$的大小？
先把分母位数变成一样，分母再保留2位估算范围，即把$\frac{441}{2.36}$变成$\frac{4410}{23.6}$；分子位数也变成一样，即把$\frac{31379}{74.06}$变成$\frac{3137.9}{74.06}\times10$
则所有分数的分母保留2位数字，即变为$\frac{9245}{14}、\frac{3137.9}{74}\times10、\frac{4410}{24}、\frac{3105}{39}$
则$\frac{9245}{14}=660、\frac{3137.9}{74}\times10=四百二十几、\frac{4410}{24}=一百八十几、\frac{3105}{39}=七十几$
3、方法3：等比修正（听说这个方法好用）
原理：分子、分母等比例变化，分数值不变
如$\frac{200}{100}=\frac{200\times(1+10\%)}{100\times(1+10\%)}=\frac{200+20}{100+10}$，你看分子分母加的数，20是10的2倍，原来的分子分母是200和100，200是100的2倍，则可以得出：分子分母加减的数的倍数是原来分子分母的倍数！
$\bigstar$则比较分数大小的时候，可以使用以下操作：
先保留3位（如$\frac{673.34}{1+6.96\%}$保留三位变为$\frac{673}{107}$，记住！是四舍五入保留3位！！！）去列式子，在列式子的时候，分子、分母原来几倍，其加减的数字也要为相同的倍数
测试一下你，$\frac{200}{100}=\frac{200-?}{100-24}$，则$?$是多少？是48
也可以大约，即如$\frac{200}{108}\approx\frac{200-?}{108-?}$
$\frac{200}{108}$约等于$\frac{200}{100}$，则分子是分母的2倍，则可以写为$\frac{200-16}{108-8}$，这样分母可以变成100，则$\frac{200-16}{108-8}$的有效数字将非常好算，因此分子减去16，分母减去8
又如$\frac{252}{98}\approx\frac{252+?}{98+?}$，你可以自己先写一下！
$\frac{252}{98}$约等于$\frac{250}{100}$，分子大约是分母的2.5倍，则可以写成$\frac{252}{98}\approx\frac{252+5}{98+2}$；或者还能这样估算，如$\frac{578}{133}$，这个看不出来约等于什么，那就直接除，发现直接除$\frac{578}{133}\approx4$，因此可以写成$\frac{578-7\times4}{133-7}$
这种估算的误差很小很小，你放心大胆去算！
$\bigstar$同时在比较分数大小的时候，还可以利用“等比修正”将两个分数的分母搞成一样的，前提是当两个分数的分母接近的时候
如比较$\frac{200}{108}$和$\frac{220}{118}$这两个分数的大小？
200是108的$2^-$倍，则如果不用约等于，则$\frac{200}{108}=\frac{200+10*2^-}{108+10}=\frac{200+20^-}{118}$
与$\frac{220}{118}$比较，肯定$\frac{220}{118}>\frac{200+20^-}{118}$
则$\frac{200}{108}<\frac{220}{118}$
$\bigstar$等比修正的应用范围：
等比修正特别是在解决疑难杂症方面，这个方法特别好用！！！
2.3 高位叠加（扩展，国考爱考很多个数相加）
$\bigstar$高位叠加就是从最高位开始加，我们从小学的都是从最低位开始算
操作：从最高位开始加起，小于10->顺；大于10 ->叠
例：5133+6052=？
5723 + 6552 =？
使用高位叠加，计算过程为：
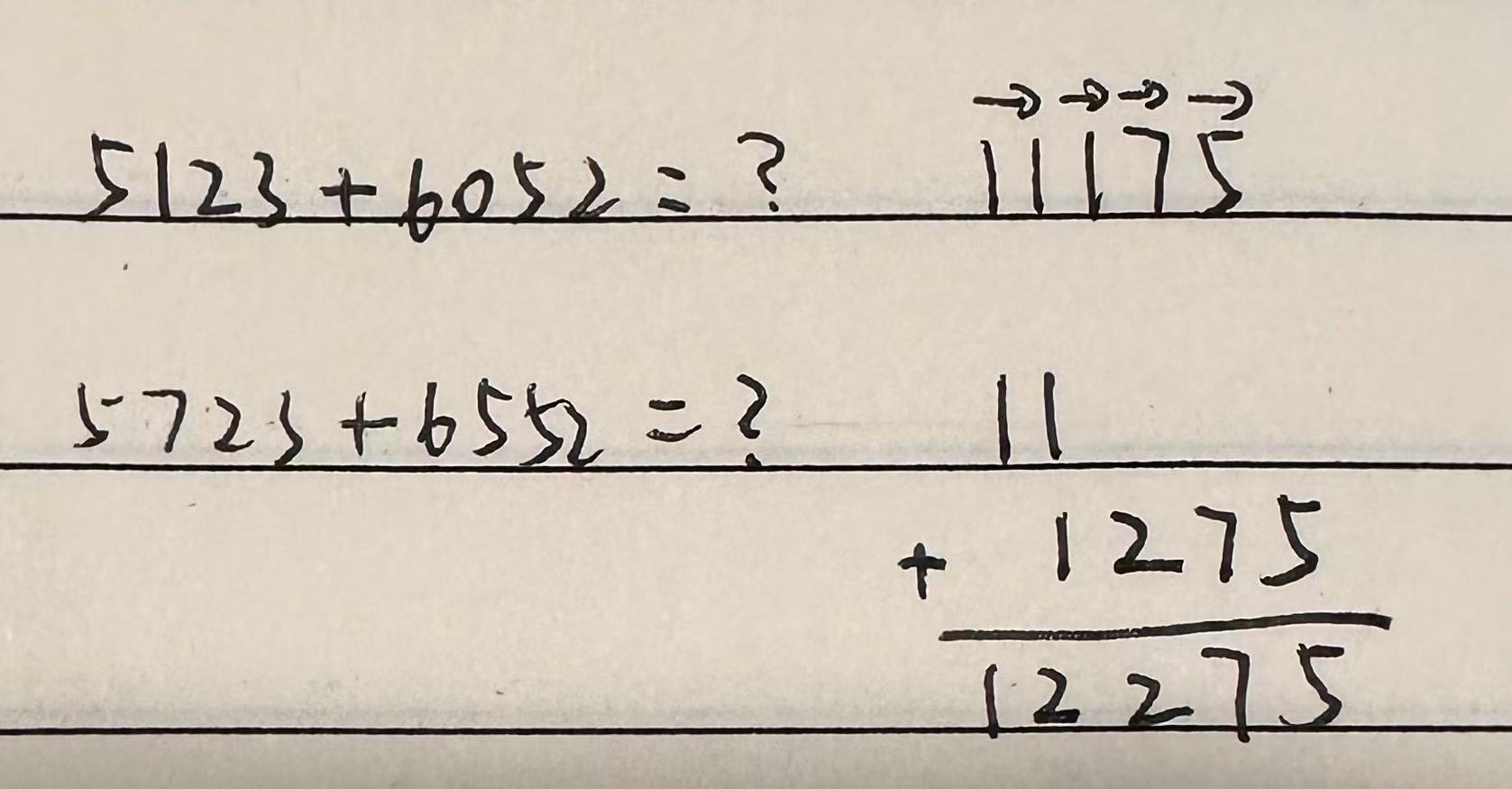
这就是高位叠加的计算过程，一定要学会！
$\bigstar$然后使用高位叠加计算多个数相加的时候，要使用“两加一估”的方法：
例1：315+315+383+417+519 = ?
A.小于1700亿千瓦时
B.1700~2000亿千瓦时
C.2000~2300亿千瓦时
D.大于2300亿千瓦时
先对最高位进行一次加法：3+3+3+4+5=18；再对第二个高位进行一次加法：1+1+8+1+1=12；此时：
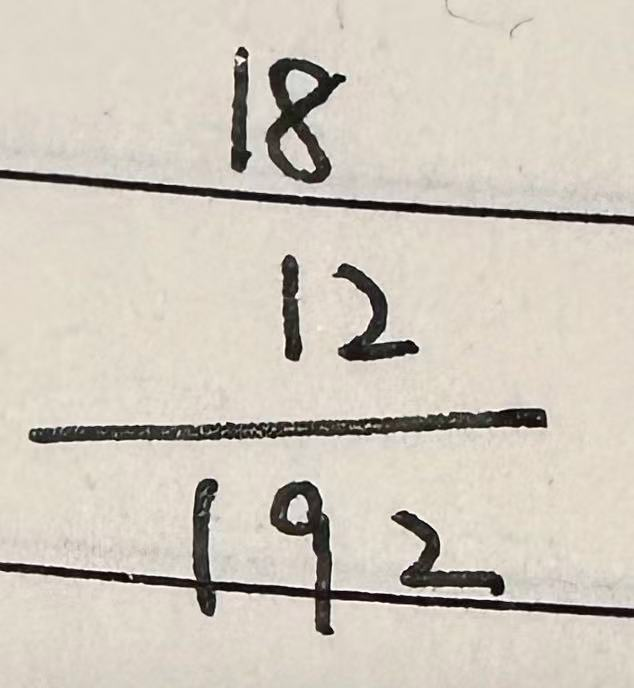
说明前几位最低是192，则排除A
对第三个高位进行估算，即第三位相加起来最多是多少？最多是9+9+9+9+9=9*5=45；撑死是45，则写成$45^-$，即过程：
即前面几位是1965不到的数，排除CD；则选B
以上就是使用高位叠加的“两加一估的”的过程，一定要学会！！！
注意！计算到哪一位，从哪一位开始估算，得根据选项判断！如下面的例1，看选项，说明算到第二位，然后从第三位开始估算！
$\bigstar$写一些例题：
例1：
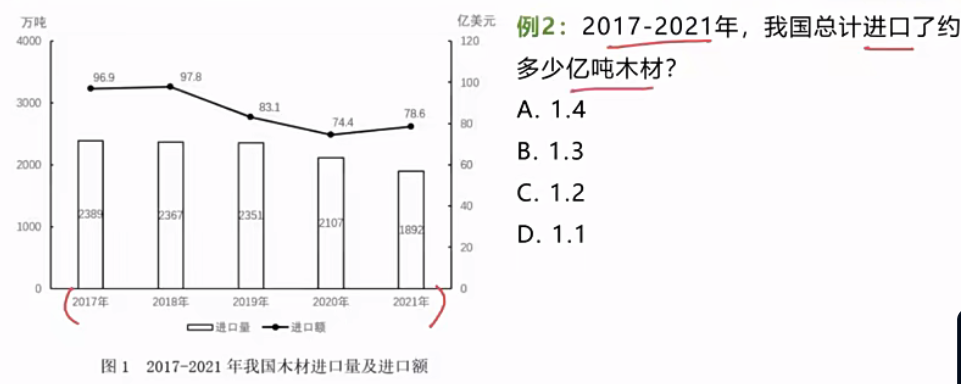
这个题选什么？
选D。利用高位叠加，能得出是前几位少于1125，只有D了。2.4 口算加减法之截位修正
方法：从左往右口算两位或三位，看下一位的进位或借位情况，进行修正
需要算到哪位就修正到哪位，例如需要算到十位，则个位也要算，因为要对十位进行修正
其实我已经很熟练了，例如加法2774+690，千位为2，百位为3，十位为6，进1，需要对百位进行修正，百位变成4，个位为4，没有进1就不用对十位进行修正
例如减法2605-2548，千位为0，百位为1，十位为6，借1，百位变为0，个位为7，借1，十位变为5
2.5 特殊数字的应用
$\bigstar$方法：一般资料分析中计算，多数不考虑位数，根据我们之前学的百化分，可以知道：
遇到 25%、2.5、25、250，想$\frac{1}{4}$、$\frac{1}{4}\times 10$等
遇到 33%、3.3、33、330，想$\frac{1}{3}$、$\frac{1}{3}\times10$等
遇到 50%、5、50、500，想$\frac{1}{2}$、$\frac{1}{2}\times10$等
遇到 12.5%、12.5、125，想$\frac{1}{8}$、$\frac{1}{8}\times10$等
遇到 14.3%、14.3、143，想$\frac{1}{7}$、$\frac{1}{7}\times10$等
遇到 16.7%、16.7、167，想$\frac{1}{6}$、$\frac{1}{6}\times10$等
$\bigstar$例题：
题1：$141178\times1.29\%=?$
A.1721 B.1821 C.1921 D.2021
这个题选什么？
选B。1.29%=12.9%/10，12.9%约等于13%（这个没想到呜呜呜），13%=1/7.7；则原式=141178/7.7/10。1411/7.7=18多少多少，则选B。这个题还有方法2
方法1用的是12.9%约等于13%。因为只看有效数字，方法2将141178约等于14，14=1/7.1，则129/7.1=18什么什么，则选B。2.6 乘法速算
1、方法1：高位乘法
例：2345$\times$6
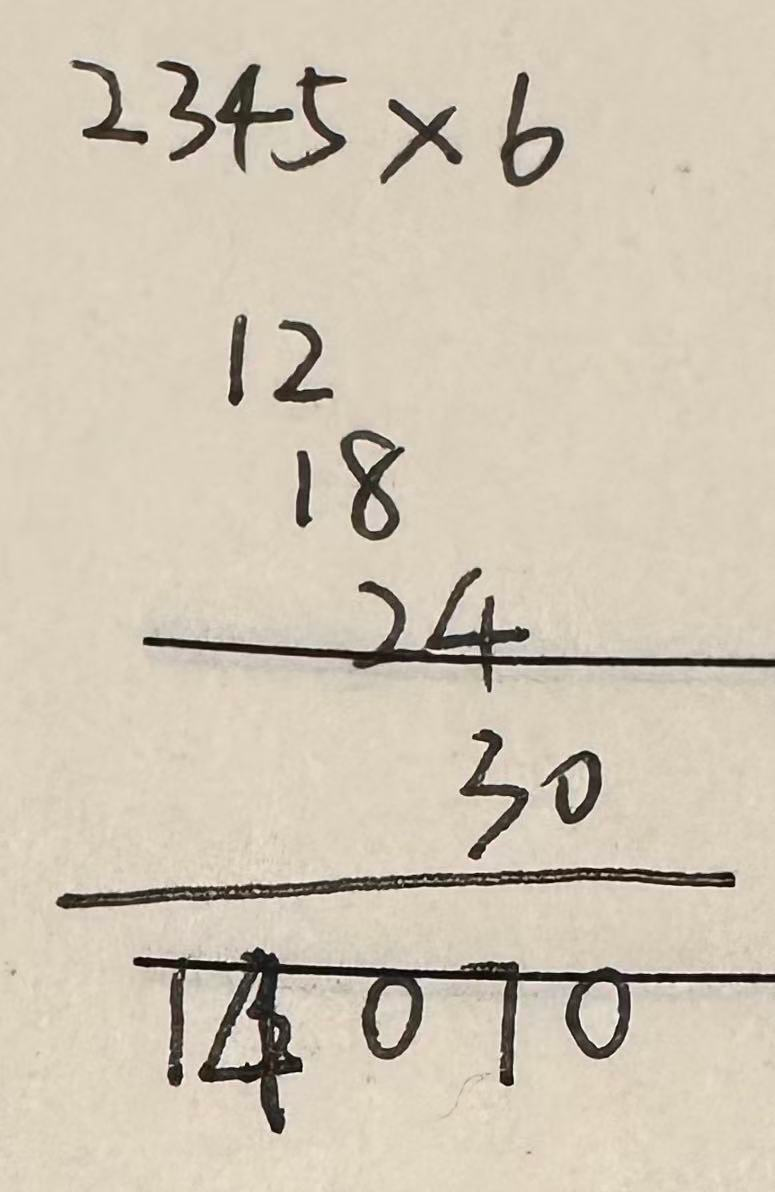
2、方法2：特殊数字法
（1）$A\times0.9$，使用错位相减，即$A\times0.9=A\times(1-0.1)$，等于本身$-$本身小数点往后移动一位
（2）$A\times1.1$，使用错位相加，即$A\times1.1=A\times(1+0.1)$，等于本身$+$本身小数点往后移动一位
（3）$A\times1.5$，即$A\times1.5=A\times(1+0.5)$，等于本身$+$本身的一半
（4）若有出现百化分对应的有效数字：
A$\times$125→$\frac{A}{8}$
A$\times$143→$\frac{A}{7}$
A$\times$167→$\frac{A}{6}$
A$\times$25→$\frac{A}{4}$
A$\times$33→$\frac{A}{3}$
A$\times$5→$\frac{A}{2}$
3、方法3：拆分法（重点）
其中有个数特别接近整十，如$19\times27=(20-1)\times27=20\times27-27$
4、方法4：口诀法（重点）
有些数拆分起来麻烦怎么办？用口诀法
例如：$23\times64$用拆分法
3 基期与现期
1、什么是基期，什么是现期？
（1）时间型：现在比过去…(以过去作为参照，衡量现在的发展)
靠前时间为基期，靠后时间为现期
例：2024年 志哥的工资比 2023年 多了好多好多
（2）对象型：谁比谁.… (比字后面作为参照)
比字后为基期，比字前为现期
例：志哥 的工资比 郭子 少了好多好多
即郭子是基期，志哥是现期
2、增长量与增长率？
增长量：关键字(增长)+具体数和单位
例：2024年 志哥的工资比 2023年增长了10元
增长率：关键字(增长)+比例(百分数、倍数、成数等)
例：2024年 志哥的工资比2023年增长了10%
增长率怎么计算？例如2018年我国电子政务市场规模3106.9亿元，同比2017年的2861.8亿元增长了百分之多少？
$增长率=\frac{3106.9-2861.8}{2861.8}=8.59\%$
3、有关同比和环比
（1）举例子
例1：2024年第一季度，同比与2023年第一季度相比，而环比与2023年第四季度相比
例2：相比2024年2月，同比与2023年2月相比，而环比与2024年1月相比
（2）关于环比的东西：
4个季度：第一季度（1-3月）、第二季度（4-6月）、第三季度（7-9月）、第四季度（10-12月）
上旬、中旬、下旬
12个月份
3.1 基期量
1、基期题型的识别
读题看时间，材料给现在，题干求过去
例1：2021年，全国城市供水总量 673.34 亿立方米，同比增长6.96%
那么2020 年，全国城市供水总量约为多少亿立方米?
例2：2022 年1-4月份，全国房地产开发投资39154亿元，同比下降2.7%
2021 年1-4月，全国房地产开发投资约多少亿元?
2、基期的公式
公式三是重点，公式一和公式二考得很少
公式一的应用：2024年，志哥的工资为120元，同比减少了20元，2023年，志哥的工资为多少元?
给的2024年，求2023年，则求基期量，为120-(-20)=120+20=140元
公式二的应用：2024年，志哥的工资同比增长20元，同比增长20%，2023年，志哥的工资为多少元?
给的2024年，求2023年，则求基期量，为$\frac{20}{20\%}$=100元
公式三的应用：如例1(P153)
公式三的来源，讲一下例1：“2021年，全国城市供水总量673.34亿立方米，同比增长6.96%，求2020年的全国城市供水总量约为？”
设2020年的全国城市供水总量为$x$，则$x(1+6.69\%)=673.34$，则$x=\frac{673.34}{1+6.69\%}$，就是公式三
3、等比修正在基期计算中的应用：主要应用于公式三
用法：分母化为100；且等比修正的分子先保留3位，加法的分母保留3位，减法的分母保留2位
以例1为例，为$\frac{673.34}{1+6.69\%}$，等比修正的分子先保留3位，加法的分母保留3位，即为$\frac{673}{107}$，直接计算673除以107也可以，但是用等比修正比较简单
化分母为100，分子约是分母的$6^+$倍，则$\frac{673}{107}=\frac{673-7\times6^+}{107-7}=\frac{631^-}{100}$，则有效数字631与C的630更接近，选它（$631^-$为什么不选620？其实我也不太懂，感觉等比修正慎用吧！）
以例3为例，为$\frac{39154}{1-2.7\%}$，等比修正的分子先保留3位，减法的分母保留2位，把2.7%直接看成3%，即约为$\frac{392}{97}$，把分母化为100，则为$\frac{397+12}{97+3}=\frac{404}{100}$，则选D
我写例1和例3都用的是“2.1 截位直除”，我觉得还是截位直除更准确点，等比修正先慎用！！！
但是等比修正算东西更快，如博客4！刷题面对不同的题好好想一想用什么
4、例1(P153)到例4(P154)都太简单了，现在来一个难的试一下：
2018年末，A省辖区各项存款余额 3051.06 亿元，同比增长4.4%。A省辖区各项贷款余额 2574.10 亿元，同比增长 9.4%。
(2019新疆兵团)2017年末，A省辖区各项存贷款余额之差约在哪个范围内?
A.440~480亿元
B.480~520亿元
C.520~560亿元
D.560~600亿元
这个题选什么？
选D。告知的是2018年，求2017年，即求基期量。截位直除这样硬算，写出来大概是570，因此选D。或者用等比修正，把分母都变成109，然后直接除，算出来也是570。公考里面的差值问题其实不多。同学们说的坑题少之又少，考察的大多数都是计算能力。
3.2 现期量
1、现期题型的识别
读题看时间，材料给现在，题干求以后
标志性特征:若保持…… 的增长量/增长率不变，……
例：如保持 2021年同比增量不变，则到哪一年第三方互联网超算服务商提供的服务市场规模将第一次超过第三方独立超算服务商?
例：根据 2018 年的增长率预测，2019 年我国电子政务市场的规模约为多少亿元?
2、现期的公式
公式一的考法：通过几年能追上谁，达到一个小目标
公式二的考法：一年即乘一次$(1+增长率)$，两年即$(1+增长率)^2$，以此类推
注意，这里的增长率也可以称为年增长率，但和年均增长率有很大区别！别搞混！
3、公式一的考法详细如下：现期追赶 (增长量不变)
例：2024年今我工资100元，同比增长20元，按照增量不变，哪年超过250元?
追定量：$所需年数(n)=\frac{现在差距}{增长量}$，若$n$不为整数，往大取整，$所求年份=基期年份+n$
例：2024年今我工资100元，同比增长20元，你145元，同比增长10元
按照增量不变，我超过你的工资?
追变量：$所需年数(n)=\frac{现在差距}{增量差距}$，若$n$不为整数，往大取整，$所求年份=基期年份+n$
4、公式二的考法详细如下：现期计算 (增长率不变)
（1）给增长率，直接代入公式计算：$现期=基期\times(1+增长率)$
（2）不给增长率，先按增长量不变估算，结果偏小选大（即增长率恒定，不代表增长量恒定）
符合选项只有一个，直接选
符合选项有多个，利滚利(分析利息产生的利息)
什么叫利滚利？例如2022年我的工资是100万，2023年我的工资是110万，按照增长率恒定，2024年我的工资为？110$\times$1.1=121万。而分析一下：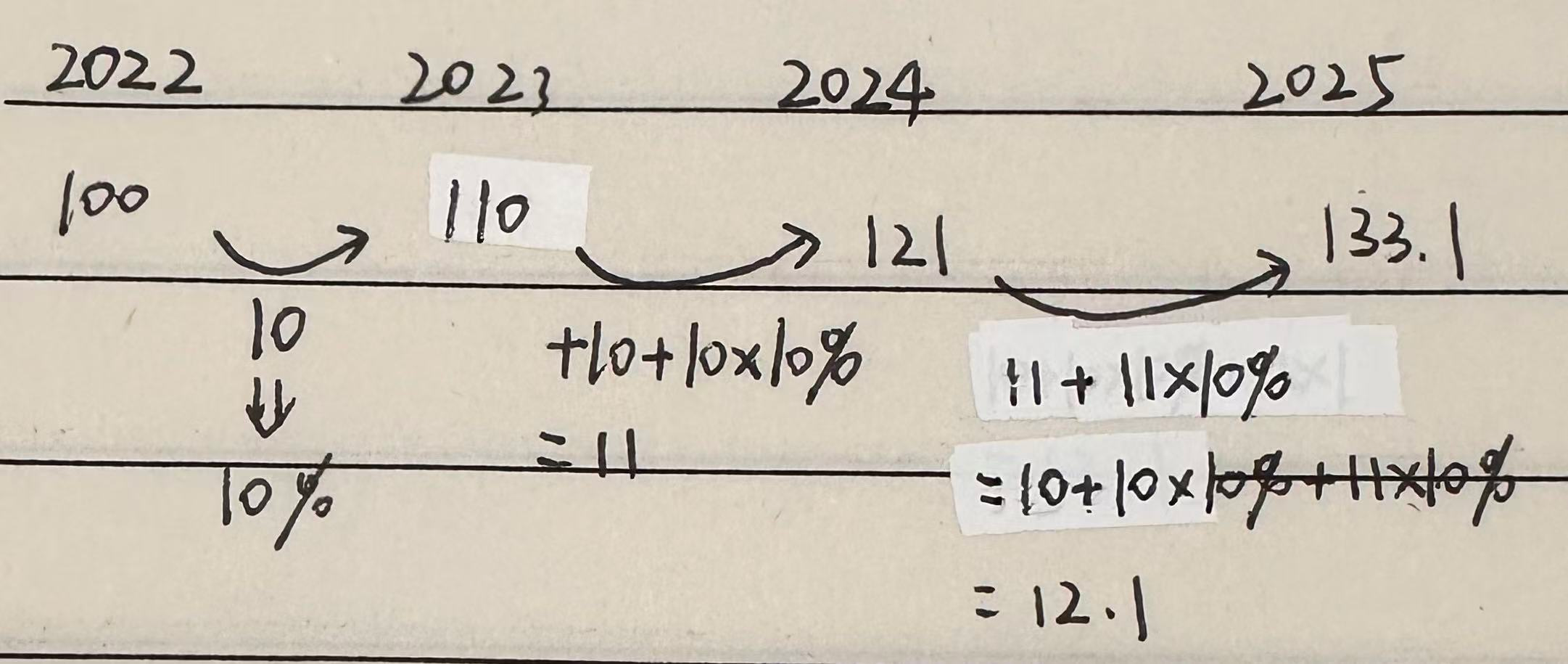
即对于2024年，由2023年的利息10产生的利息为10$\times$10%；对于2025年的10+10$\times$10% +11$\times$10%，10是增长量，10$\times$10%是上一年由利息产生的利息，而由2024年的利息11产生的利息为11$\times$10%
分析利息产生的利息，可以选出选项；第一年由利息产生的利息为1，第二年由利息产生的利息为2.1，第一年由利息产生的利息都特别小，由这个可以选出选项（为啥呢？可以看博客6的题2）；但是第二年要根据这个利息的利息选出选项的话，可能不太行哦！
5、对于例2我有话要说：
（1）增长率恒定，不代表增长量恒定。因为每年的基期不同，而$增长量=基期\times增长率$
（2）例题2有2种方法：
$\bigstar$方法1：$现期=3106.9\times(1+8.6\%)\approx3107\times(1+10\%-1.4\%)\approx3107\times1.1-3107\times0.014$，3107$\times$1.1的打草稿可以这样简化：
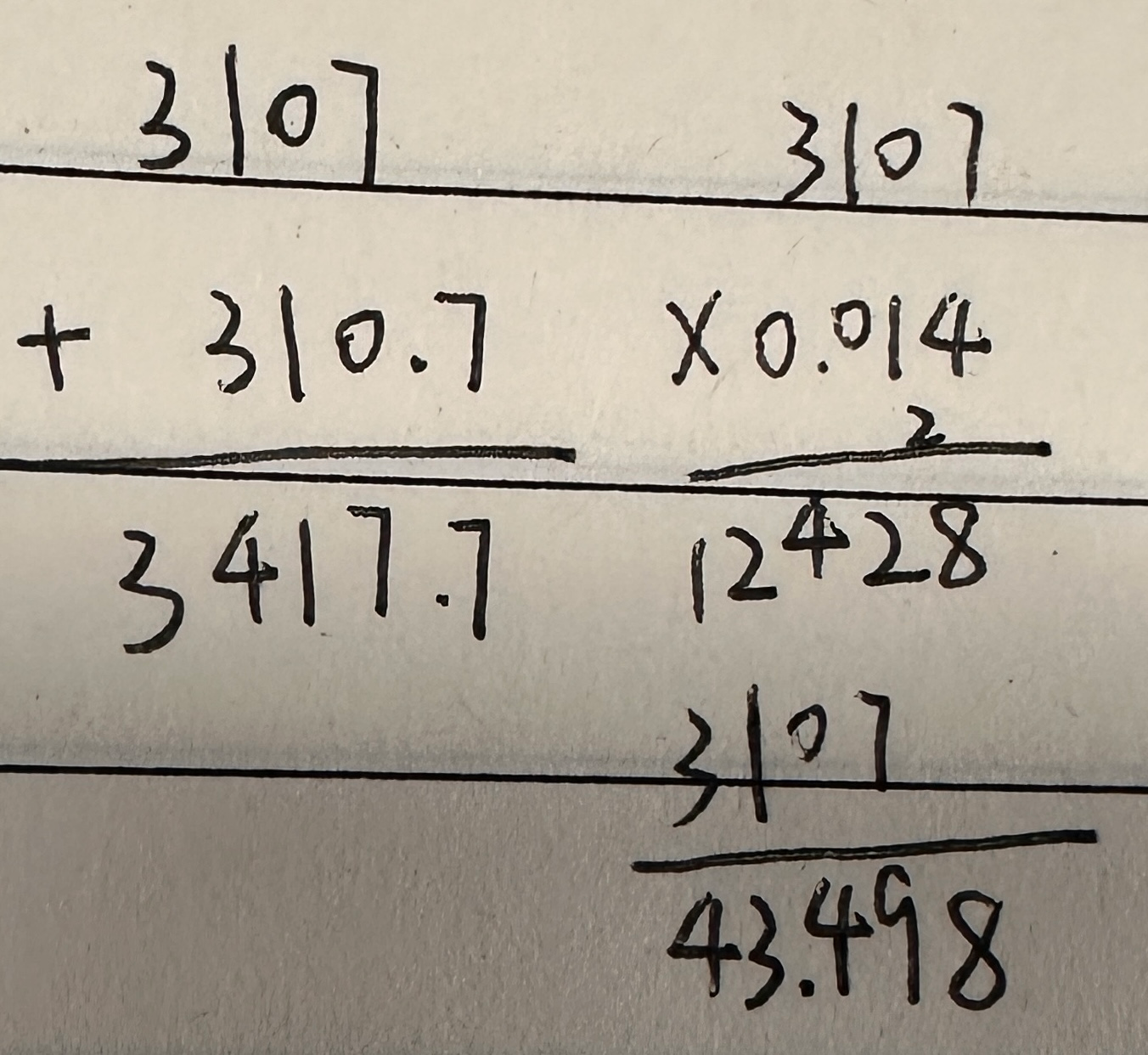
结果为3417.7-43，约在三千三左右，选B
$\bigstar$方法2：
$现期=基期\times(1+增长率)$，则$现期-基期=现期\times增长率$
3106.9$\times$8.6%应该是2开头的数，对于选项，现期-基期后，A是1开头的数，B是2开头的数，C是3开头的数，D是4开头的数，则这样可以锁定B
6、对于博客4（2），出一些例题：
题1：
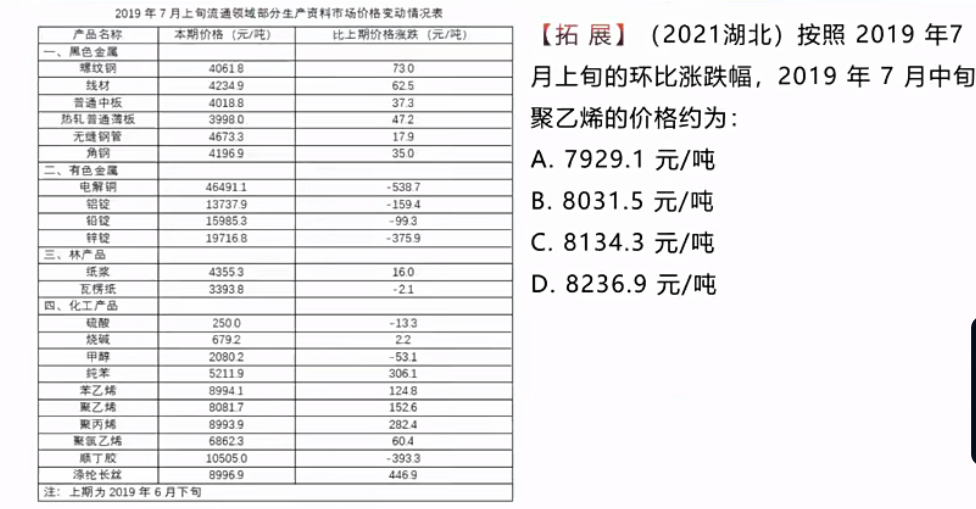
这个题选什么？
选D。按照博客4（2）的方法，不给增长率，先按增长量不变估算，结果偏小选大。按增长量不变计算，为8081.7+152.6=8234.3，由于结果偏小，则只能选D。
题2：
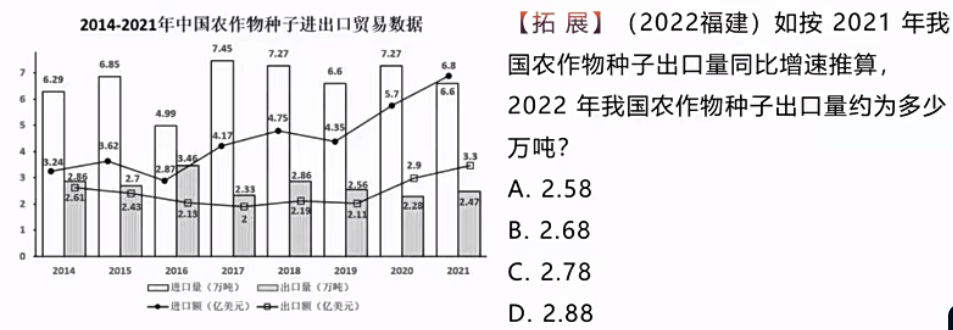
这个题选什么？
选B。按照博客4（2）的方法，不给增长率，先按增长量不变估算，结果偏小选大。增长量为2.47-2.28=0.19，按增长量不变计算，为2.47+0.19=2.66，由于结果偏小，则只能选BCD。
如何排除CD呢？即看它由利息产生的利息，B由利息产生的利息为2.68-2.66=0.02；C由利息产生的利息为2.78-2.66=0.12；D由利息产生的利息为2.88-2.66=0.22；
增长量为0.19， 增长率0.19/2.47一定是一个特别小的值，而C的0.12占0.19的50%了，增长率怎么可能是50%，D的0.22是0.19的100%还多，因此只能选B。
4 一般增长率
1、倍数与增长率
（1）倍数：A是B的几倍，即$倍数=\frac{A}{B}$
（2）增长率：A比B的增长率（也可以说A比B多几倍），即$增长率=\frac{A-B}{B}=\frac{A}{B}-1$
即增长率=倍数-1；倍数=增长率+1
2、成数的易错点：
3成多，即30%<X<40%；如35%可以形容成3成多
超过3成，即X>30%
3、关于番数
遇番数化倍数，翻n番为原来的$2^n$倍
例如：100翻5番为3200；200变800，翻了2番
2024年、2023 年志哥工资分别为199元、100元,2024年志哥工资对比上年是否实现了翻番?
是否实现翻番，即至少需要翻1番，即志哥的工资至少得是100*2=200，因此没有实现翻番
4、百分数：表示两个量的比例关系，用除法计算
例：男生 300 人，全班500人，则男生占全班的60%
百分点:表示百分数的变化，用减法计算
例：男生占比 60%，女生占比40%；男生占比比女生多60%-40%=20%，即20个百分点；可以这么说，60%比40%多20个百分点
5、增幅：就是增长率
有正有负：增幅为正代表增长，增幅为负代表减少
例：2024 年志哥工资同比增长10%→增幅为10%
2024 年志哥工资同比减少10%→增幅为-10%
比较时：有负号带负号
例：A上升10%，B下降20%，C下降30%，D上升20%
增幅低于 20%的有？ABC，A是10%，B和C都是负数，肯定小于20%
增幅最小的是？C
6、降幅：只有下降时，才能称为降幅
例：2024 年志哥工资同比减少10%→降幅为10%
比较时：只看数字(绝对值)
例：A上升10%，B下降20%，C下降30%，D下降40%
降幅超过 15%的有？BCD；A不是降幅，只有BCD是降幅
降幅最小的是？B
7、变化幅度：上升、下降均为变化
比较时：只看数字(绝对值)
例：A上升10%，B下降20%，C下降30%，D上升20%
即A变化幅度为10%，B变化幅度为20%，C变化幅度为30%，D变化幅度为20%
变化幅度超过 5%的有？ABCD
变化幅度最大的是？C
变化幅度最小的是？A
4.1 计算
1、增长率的识别
关键词(增长 )+比例(百分数、成数、倍数)
增长率又名增速、增幅、增长最快/慢、增长幅度、增值率等
例：2021 年，全国羊肉产量同比增长率约为:
例：2011-2018年间，我国海洋主题公园非门票收入同比增速超过10%的年份有几个?
例：2014-2017年，中国保险行业原保险保费收入同比增速最高的年份是:
2、增长率的公式
$增长率=\frac{增长量}{基期}=\frac{增长量}{现期-增长量}=\frac{现期-基期}{基期}$
3、题型
（1）给现期增长率，与百分点的关系，计算基期增长率
第一步：看加减，看百分点前表述“高减低加”
提高：上升、增加、扩大、提升 等
降低：下降、减少、缩小、收窄 等
第二步：看规则，再往前看表述“按规办事
增速/增幅：有负号带负号
计算降幅：只计算数字(绝对值)
例1：2024 年志哥工资的同比增长率为10%，增幅比上年提高了 3 个百分点，则2023 年志哥工资的同比增长率为？
解：为10-3=7%
例2：2024 年志哥工资的同比下降10%，降幅比上年扩大了3个百分点，则2023 年志哥工资的同比增长率为？
解：2023年降幅为10-3=7%，则同比增长率为-7%
例3：2024 年下降 17%，增速比上年同期提高5个百分点，则2023年增长率为？
解：为-17-5=-22%
（2）给现期、基期、增长量，任意两个，计算增长率
利用增长率的公式$增长率=\frac{现期-基期}{基期}$，分子、分母其中给一个，做减法（减法不用算的很精确，可以使用“2.4 口算加减法之截位修正”）求另外一个
还有，如果给的是现期、基期，可以根据公式$增长率=\frac{现期}{基期}-1$来计算，但是由于最终结果要-1，可能需要换一下脑子计算，例如现期=18982.8，基期=15915.5 求增速，$\frac{18982.8}{15915.5}\approx\frac{189}{16}\approx1.2$，减去1后为0.2，即使用公式$增长率=\frac{现期}{基期}-1$的时候，最终结果看$\frac{现期}{基期}$计算出来的数的小数点后的数，而不是直接看有效数字，这样还需要看$\frac{现期}{基期}$估算后的小数点在第几位，比直接看有效数字难，因此最好还是用公式$增长率=\frac{现期-基期}{基期}$来计算
（3）特定增长率：给现期、基期，判断增长率大于某一数值的有几个
例：2011-2018 年间，我国海洋主题公园非门票收入同比增速超过 10%的年份有几个?
$\bigstar$增长率为整十的数字(10%、20%、50%等)→转化倍数，速算倍数
第一步：转化倍数。是几倍=增长率+1；例如增长率超过10%，转化为倍数，即增长率>1.1倍$\times$基期
第二步：速算倍数。方法如下：
$\bigstar$增长率为非整十的数字(2.7%、4%、15%等)→回归公式，保留3位
对应题如下：
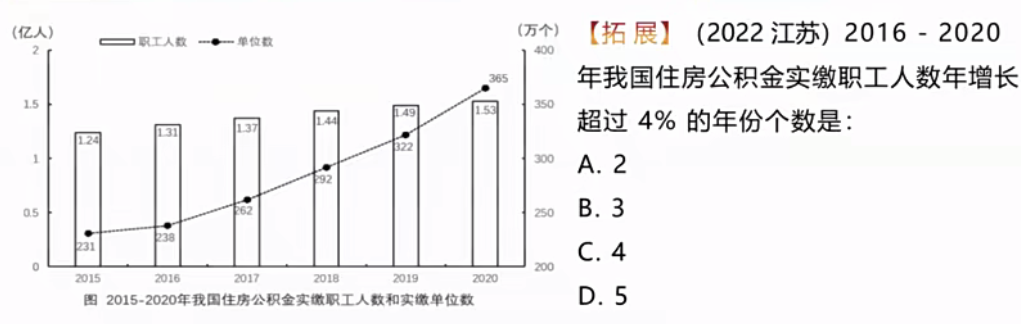
这个题选什么？
选B。用公式直接计算；2016的增长率为(1.31-1.24)/1.24，即计算700/124，发现第一位超过4，可以；2017的增长率为(1.37-1.31)/1.31，即计算600/131，发现第一位是5，超过4，因此可以；以此类推，发现2018年的也行，其他都不行，选B。这样发现公式计算其实不难！别害怕
4.2 比较
1、题型为：给现期、基期，比较增长率
（1）情况一：现期、基期倍数差异明显，比较倍数
由公式增长率=倍数-1可以知道，倍数越大，增长率越大
怎么算是现期、基期倍数差异明显？如下图：
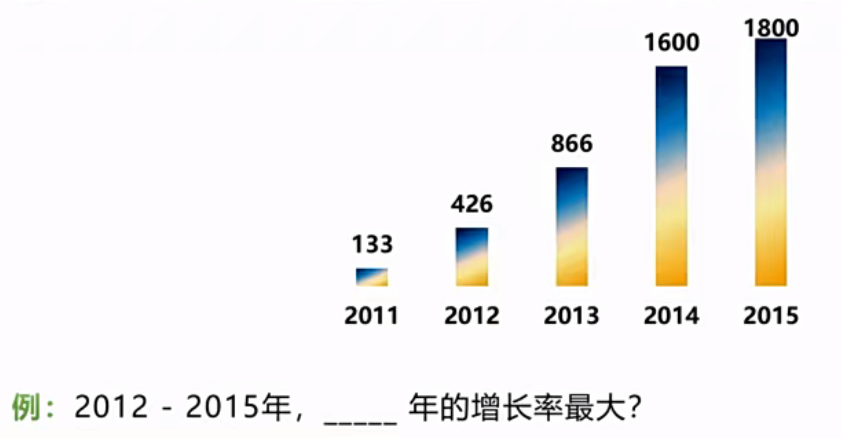
能看出2012年是2011年的3倍多；2013年是2012年的2倍多；2014年是2013年的2倍少一点；2015年是2014年的1倍多一点
则2012年的同比倍数大，则2012年的增长率大
（2）情况二：现期、基期倍数差异不明显，比较增长率
什么叫做现期、基期倍数差异不明显？如下图：
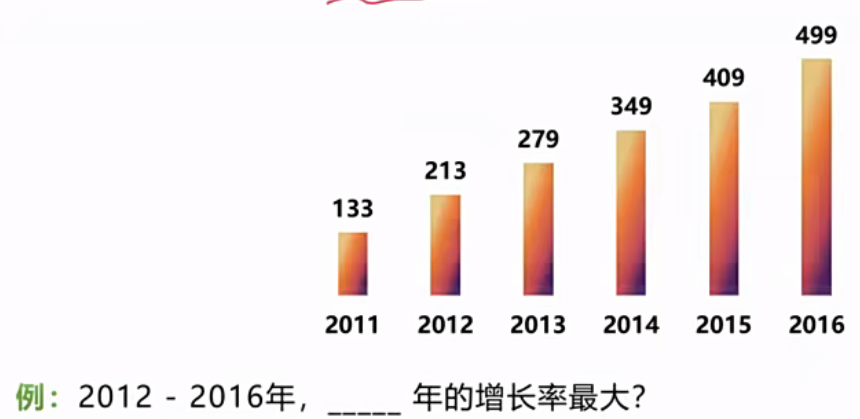
先按照增长量分析：2012年增长量为80，2013年的增长量为66，2014年的增长量为70，2015年的增长量为60，2016年的增长量为90
$增长率=\frac{增长量}{基期}$，如果增长量大，基期小，则增长率一定大
2012年的基期最小，为133，如果其他年份的同比增长量小于2012年，则同比增长率肯定小于2012年的；则排除2013年、2014年、2015年的
这时候只要对比2012年和2016年的增长率即可，直接截位直除，则2013年的增长率最大
2、拓展题型：给现期、增长量，比较增长率
公式：$增长率=\frac{增长量}{现期-增长量}=\frac{1}{\frac{现期}{增长量}-1}$
方法：直接比较$\frac{增长量}{现期}$，结果越大，增长率越大（仅限比较的时候使用，计算不能用）
例题：
2022 年，S省各级 12315 工作机构共接收诉求 220.4万件，同比增长 21.41%。其中，投诉 55.6万件、举报 26.3 万件、咨询 138.5 万件，比上一年分别增加 14.0 万件、8.9 万件、16.0 万件。
[拓 展]将S省各级12315工作机构接收的投诉、举报和咨询三类诉求量按2022年同比增速从高到低排序，以下正确的是:
A. 投诉量、举报量、咨询量
B. 咨询量、投诉量、举报量
C. 举报量、咨询量、投诉量
D. 举报量、投诉量、咨询量
这个题选什么？
选D。比较增长量/现期，即比较14/44.6、8.9/26.3、16/138.5的大小，计算后14/44.6为0,2，8.9/26.3为0.3，16/138.5为0.1；增长量/现期越大，则增长率越大，因此选D。5 增长量
1、增长量的识别
关键词(增长)+具体数值+单位，增长最多/少
例：2022年1-7月份，全国城乡居民生活用电量比2021年1-7月份约多亿千瓦时
例：2011-2018 年全国文物机构数增加最多的年份是：
例：2018 年，下列三种产品出口金额增长值从大到小的顺序排列正确的是：
2、增长量的公式
公式一：增长量=现期-基期
公式二：增长量=基期$\times$增长率
公式三：增长量=$\frac{现期}{1+增长率}\times$增长率
公式三由“现期=基期$\times(1+增长率)$”得来
5.1 计算
1、题型1：给现期、基期，计算增长量大于某一数值的有几个
$\bigstar$方法：做差，算到精度上的数字
等于，看下一位修正
大于，一定满足
小于，一定不满足
$\bigstar$例：2011-2015年，志哥工资分别为133元、156元、184元、215 元、254 元。则2012-2015年，志哥工资同比增长量超过30元的有几年?
上面那个方法什么意思呢？就是题中说“超过30元”，30精确到了十位，则我们直接从左往右计算，计算到十位，暂时不修正
156-133的十位是2，则其增长量肯定不超过30；
184-156的十位是3，对比30比不出来，此时要算到个位，并修正十位，个位为8，且要修正十位，十位-1即2，则28<30，则其增长量肯定不超过30；
215-184的百位是1，十位是3，计算十位的时候修正百位为0，由于百位十位组成的3无法判别是否比30大，则算到个位，此时要修正十位，个位为1，不需要修正十位，31>30，则增长量超过30
254-215的百位为0，十位为4，就算修正也至少是3，则肯定增长量超过30
以上例子用于熟悉方法
$\bigstar$例题：
（1）例1（P165）写一下，作为这个题型1的基础题
（2）扩展题：
这个题选什么？
选C。2012-2015年很好算，只有2015年满足。坑在于2011年，使用现期+增长率可以计算增长量。为687.7/(1+6.4%)*6.4%=687.7/1.064*0.064=687.7/1064*64=0.6几*64，因为64*0.5>30，因此0.6*64>30，2011年也满足。因此选C。
共4次
$\bigstar$基期的选取(除江苏省考以外的考试)：
普通表述：现期最后一年，基期第一年，年份差直接相减
例：2016-2020年间，…的年均增量为:
特定表述(五年规划)：现期最后一年，**基期前推一年**，年份差必须为5
例：十三五期间(2016-2020年)，……的年均增量为:
基期2016年前推一年为2015年，则增长次数为2020-2015=5年
基期前推一年：如十三五期间(2016-2020年)，从2016年初开始统计到2020年末
把2016年初代替为2015年末，统计到2020年末，则增长次数一共2020-2015=5年，且也要2020年的现期-2015年的基期
**十三五期间的基期为“三五十五”，即基期为2015年；十二五期间的基期为“二五一十”，即基期为2010年**
而普通表述2016-2021年间，都是从2016年末-2020年末，即增长次数一共2020-2016=4年，且是2020年的现期-2016年的基期
3、题型3：给现期、增长率，计算增长量
$\bigstar$题型识别：
例：2024 年志哥工资100 元，同比增长10%，2024 年志哥工资同比增长了多少元?
例：2024 年志哥工资100 元，同比减少10%，2024 年志哥工资同比减少了多少元?
$\bigstar$方法：
涉及公式：增长量=$\frac{现期}{1+增长率}\times$增长率，由现期=基期$\times(1+增长率)$，$增长量=基期\times增长率$得来
设增长率为$r$，第一步，$|r|=\frac{1}{N}$，算出$r$对应的分数$\frac{1}{N}$，即算出$N$；第二步，$增长量=\frac{现期}{N+1}$，$减少量=\frac{现期}{N-1}$
$\bigstar$常用百化分：
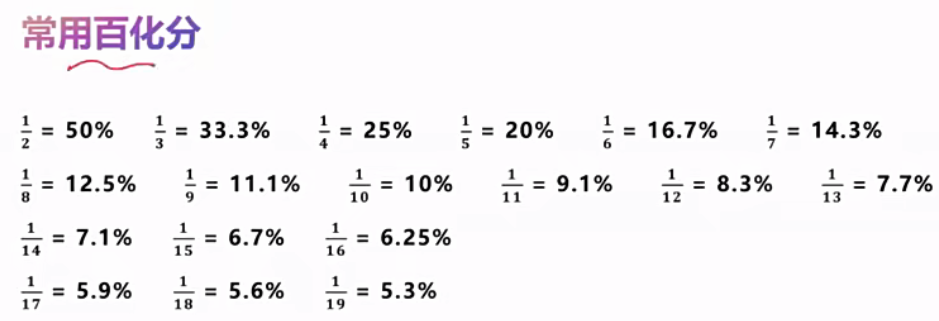如何记忆？志哥CP记忆法
记忆$6.7\%=\frac{1}{15}$，也可以记成$15\%=\frac{1}{6.7}$
注意一下！13%，对应大7，不能写成$13\%=\frac{1}{7}$，得写$13\%=\frac{1}{大7}$，可以写成$13\%=\frac{1}{大于7.5的数}$，如写成$13\%=\frac{1}{7.7}$
$\bigstar$常用百化分能解决哪些百分数？
1% 2% 3%(由$\frac{1}{3}=33.3\%$可知$3\%=\frac{1}{33.3}$) 4% 5% 5.几% 6.几% 7.几% 8% 9% 10% 11%(由$9\%=\frac{1}{11}$可知$11\%=\frac{1}{9}$) 12% 13% 14% 15% 16% 17% 18% 19% 20% 25% 33.3% 40% 50% 五十几%(用放缩法，如$53\%=5.3\%*10=\frac{10}{19}$) 六十几% 七十几% 83% 91% **这么一看，不是分数全覆盖了嘛！**
但是例如18.4%和18.9%这类数字，也可以百化分。如18.4%，可以$\approx18\%$，即等于$\frac{1}{5.6}$；例如18.9%，可以$\approx19\%$，即等于$\frac{1}{5.3}$；即依据$18.4\%\approx18\%$与$18.9\%\approx19\%$，可以看出估算的时候得**四舍五入**！
$\bigstar$化百分数为分数的常用方法：
（1）放缩法：利用与背过的百分数的倍数的关系，实现百化分
例：$67\%=?$ 用大$6$是$\frac{1}{15}$，即$6.7\%=\frac{1}{15}$，则$67\%=6.7\%*10=\frac{10}{15}=\frac{2}{3}$
（2）取中法：如果遇到百分数左右难取舍，取中即可
例：$18.4\%=?$ $18.4\%$在我们熟悉的百分数$16.7\%$与$20\%$之间，即在$\frac{1}{6}$和$\frac{1}{5}$之间，取中则取$18.4\%$为$\frac{1}{5.5}$
（3）直除法：如果遇到百分数实在想不起来，那么请记住：$N=\frac{100}{百分号前的数字}$，直除法需要算出小数点后一位
$\bigstar$（前提：百化分困难的情况下）介绍一个不用$增长量=\frac{现期}{N+1}$公式的方法，即直接用公式增长量=$\frac{现期}{1+增长率}\times$增长率，但是要使用点技巧
例如例7(P167)，为$\frac{8996}{1+68.37\%}\times68.37\%=\frac{90}{17}\times68=90\times4=360$，则对应选项C
4、题型4：给现期、增长率，计算增长量的倍数
$\bigstar$题型识别：
例1：2024 年志哥工资200元，同比增长50%，2024年郭子工资100元，同比增长5%。则2024 年志哥工资同比增长量是郭子的多少倍?
例2：2024 年志哥工资200元，同比增长10%，2024年郭子工资100元，同比增长5%。则2024 年志哥工资同比增长量是郭子的多少倍?
$\bigstar$方法：
（1）增长率相差10个百分点以上，（这种情况没有技巧，只能老老实实地分别算增长量）分别百化分计算增长量，再求倍数
（2）增长率相差10个百分点以内，增长量倍数$\approx$现期倍数$\times$增长率倍数
对于方法(2)，由题型识别的例2，可以解释一下：
倍数为$\frac{\frac{200}{1+10\%}\times 10\%}{\frac{100}{1+5\%}\times5\%}$，对于$\frac{1+10\%}{1+5%}=\frac{1.1}{1.05}$，$\frac{1.1}{1.05}$的倍数关系不明显，因此倍数$\frac{\frac{200}{1+10\%}\times 10\%}{\frac{100}{1+5\%}\times5\%}\approx\frac{200}{100}\times\frac{10\%}{5\%}$，即增长量倍数$\approx$现期倍数$\times$增长率倍数成立
$\bigstar$例题：
题1：
这个题选什么？
选C。由于增长率相差10个百分点以内，因此增长量倍数约等于现期倍数乘以增长率倍数。28920/20774约等于28/20=1.4，9.6/7.9约等于9.6/8=1.2，1.4*1.2约为1.68，则选C。5.2 比较
1、题型1：给现期、基期，比较增长量
（1）情况1：材料为柱状图
方法：看柱状图里的柱子的高度差，高度差越大，增长量越大
（2）情况2：材料为折线图
方法：看倾斜度，倾斜度越大，增长量越大。例如：
因为$倾斜度=\frac{\Delta y}{\Delta x}=\frac{增长量}{固定值}$，因此可以通过倾斜度比较增长量
（3）情况3：图不明显或材料仅为数字
2、题型2：给现期、增长率，比较增长量
（1）情况1：现期大，增长率也大
则增长量一定大，因为$增长量=\frac{现期}{1+增长率}\times增长率=\frac{现期}{\frac{1}{增长率}+1}$，因此增长率大，则分母小，现期大，则分子大，总体来说增长量就大
（2）情况2：现期大，增长率却小
先分别看现期和增长率的倍数：
90%以上的题：如果现期的倍数大于增长率的倍数，则看现期，现期大则增长量大；如果现期的倍数小于增长率的倍数，则看增长率，增长率大则增长量大
若现期和增长率的倍数接近（即第一位有效数字相同），则用百化分比较，即$a=\frac{1}{N_a}，增长量_a=\frac{A}{N_a+1}$，$b=\frac{1}{N_b}，增长量_b=\frac{B}{N_b+1}$，截位直除，看谁的增长量大
注意点1：在看现期和增长率之前，如果发现有一个X是“下降了25%”这种，则增长率为负，即增长量为负，则X的增长量一定是最小的（如果没有其他负的增长量的话）
注意点2：例如邮政业收入82.8亿元，同比增长16.7%；配送、加工、包装业收入98.9亿元，同比增长6.4%。谁的同比增量大？发现虽然增长率倍数大于现期倍数，但是配送现期大于邮政业现期，配色增长率却小于邮政业增长率，此时还能看增长率倍数和现期倍数吗？可以的！忽略“现期、增长率”谁大谁小，只看现期和增长率倍数谁大谁小！！！
（3）易错点：
$\bigstar$增长量可以是负数，比较谁的增长量小，肯定是负数最小，一定别忘了负数
$\bigstar$若比较的是变化量，则看绝对值，必须百化分比较（而不能用“比较增长量，先看现期和增长率的倍数，如果现期的倍数大于增长率的倍数，则看现期，现期大则增长量大”，这个原则完全不适用！比较变化量只能直接计算）
例如：2024 年志哥工资为 110元，同比增长10%；郭子为 100 元，同比减少10%，则2024年谁的工资同比变化量大?
即比较$\frac{现期}{N+1}与\frac{现期}{N-1}$的大小，即$\frac{110}{11}$与$\frac{100}{9}$的大小，最后$\frac{100}{9}$更大
6 比例公式初相识
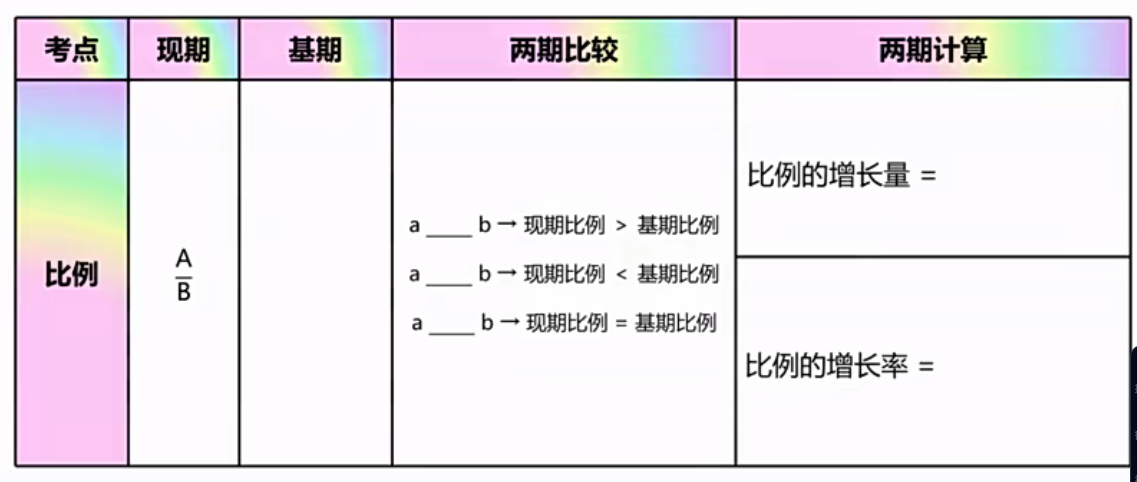
1、考一下自己的记忆力：（答案在下面）
6.1 现期比例
1、什么是现期比例？
设一个现期为A，增长率为a，另一个现期为B，增长率为b，则现期比例为$\frac{A}{B}$
6.2 基期比例
1、公式：设一个现期为A，增长率为a，另一个现期为B，增长率为b，则基期比例为（还可以称为$\frac{A}{B}$的基期）：
$\frac{A的基期}{B的基期}=\frac{\frac{A}{1+a}}{\frac{B}{1+b}}=\frac{A}{B}\times\frac{1+b}{1+a}$
记忆口诀：在现期比例后，写一个小尾巴，1+，1+，增长率交叉对应
6.3 两期比例比较
1、设一个现期为A，增长率为a，另一个现期为B，增长率为b，$\frac{A}{B}$与$\frac{A}{B}\times\frac{1+b}{1+a}$比大小：
它俩比大小，取决于$\frac{1+b}{1+a}$，如果它大于1，则现期小于基期；如果它小于1，则现期大于基期；如果它等于1，则现期等于基期
两期比例比较，看a和b的大小：
a>b → 现期比例>基期比例 → 今年比例同比上升
a<b → 现期比例<基期比例 → 今年比例同比下降
a=b → 现期比例=基期比例 → 今年比例同比不变
6.4 两期比例的增长量
1、公式：设一个现期为A，增长率为a，另一个现期为B，增长率为b，现期比例-基期比例：
$\frac{A}{B}-\frac{A}{B}\times\frac{1+b}{1+a}=\frac{A}{B}\times(1-\frac{1+b}{1+a})=\frac{A}{B}\times\frac{1+a-(1+b)}{1+a}=\frac{A}{B}\times\frac{a-b}{1+a}$
记忆口诀：与基期比例很像，区别在小尾巴的分子，增长量是做差，做差为$(a-b)$
6.5 两期比例的增长率
1、公式：设一个现期为A，增长率为a，另一个现期为B，增长率为b，比例的增长率=倍数-1=$\frac{现期比例}{基期比例}-1$：
$\frac{\frac{A}{B}}{\frac{A}{B}\times\frac{1+b}{1+a}}-1=\frac{1}{\frac{1+b}{1+a}}-1=\frac{1+a}{1+b}-1=\frac{1+a-(1+b)}{1+b}=\frac{a-b}{1+b}$
记忆方式：只能硬记
7 比重
1、比重的识别：
关键字（占）：A占B的比重；B 中 A的占比；利润率、增长贡献率也是比重
例：以下饼图中，最能准确反映 2020 年信息技术服务实现收入中，电子商务平台技术服务收入(黑色)云服务、大数据服务收入(竖线)和其他收入(白色)占比关系的是:
例：2020 年前三季度，G省智能机器人产业的总体利润率($利润率=\frac{利润总额}{营业收入}$)约为:
例：2019 年江苏省“三新”经济增加值占全省地区生产总值的比重是:
2、比重的公式：
（1）$现期比重=\frac{A(现期的部分)}{B(现期的总体)}$
（2）$基期比重=\frac{A}{B}\times\frac{1+b(总体的增长率)}{1+a(部分的增长率)}$
（3）$两期比重差(增长量)=\frac{A}{B}\times\frac{a-b}{1+a}$
（4）$利润率=\frac{利润}{收入}$
（5）$增长贡献率=\frac{部分的增长量}{总体的增长量}$
注意，对于利润率，我们这一节是资料分析，在资料分析中利润率分母为收入；而在上一次的数量关系中，利润率分母为成本
注意，现期比重和基期比重都是部分比总体
7.1 现期比重
1、如何求现期比重？
$\bigstar$识别：
先看题目中有几个时间。题目中只有一个时间，则要么考现期，要么考基期
然后看给的时间，求什么时间的什么东西。如下面情况1的例题，给的2024年的东西，求2024年的东西，说明考的现期
找关键字。发现“占”字，则考的比重。
$\bigstar$题型：
情况1：给部分、总体，直接除
例：2024 年志哥家庭总收入为100元，其中，志哥收入为20元。2024 年志哥收入占家庭总收入的？
情况2：给部分、不给总体，用类比(总体相同，部分几倍，比重几倍)
例：2024 年志哥媳妇收入10元，占家庭总收入10%，志哥收入为20元，2024 年志哥收入占家庭总收入的？
方法1：$\frac{10}{10\%}=100，\frac{20}{100}=20\%$。这样做不行，因为太慢了！
方法2：媳妇的10占家庭总收入的10%，则类比分析，志哥的20占家庭总收入的$\frac{20}{10}\times10\%=20\%$。这个方法更快！用这个！
2、对于例4，因为需要把利润总额全部加起来，如果要直接计算，就浪费时间了，因此差不多计算即可，因为其中两个0.几的数很小，忽略不计，其他就是40-8，则利润总额大约是32，计算时看成320，总收入计算时看成33，则320/33，有效数字为9，选C
3、补充一题关于题型情况2的例题：
这个题选什么？
选D。用情况2提到的类比法，题目中说4893.4占16.1%，则4940.7肯定占大于16.1%，且和16.1%相近，排除AB。保险的话，算了一下4940.7/4893.4，选项差距大，我用494/49计算的，算出来1.009，约等于1.01，1.01*16.1%=16.26%，则选D。
我其实这题计算了东西，老师说会浪费时间，就慢了，后续练题的时候，看看要是算会对整体时间影响多少，要是影响不大，就算。我感觉是因人而异！
4、扩展题型：现期比重：求总体
认知过程：时间→ 1个 → 现期 → 关键字→ 占、总 → 给部分、比重 → 根据公式：$总体 =\frac{部分}{比重}$
公式：$总体 =\frac{部分}{比重}$
例：2024 年志哥收入为 20元，占家庭总收入20%，2024 年志哥家庭总收入为多少元？
5、注意一下例2，没必要把$\frac{14.2}{36.3\%}$这种复杂的数字全抄下来，直接在草稿纸上写截位直除的$\frac{142}{36}$即可，这样能节省时间！！！
6、扩展题型：现期比重：求部分
认知过程:时间 → 1个 → 现期 → 无关键词 → 给总体、比重 → 根据公式：部分 =总体 $\times$ 比重
公式：部分 = 总体 $\times$ 比重；涉及到乘法，用百化分
例：2024 年志哥家庭总收入为100元，其中，志哥收入占家庭总收入20%。2024年志哥收入为多少元？
7、扩展题型：
看比例的时候，有一些比例比较好看出来，比如$\frac{1}{2}、\frac{1}{3}、\frac{1}{4}$：
优先看部分与总体的比例，看不出来再看部分与部分之间的比例
8、对博客1的题型情况1，我要扩展一题：
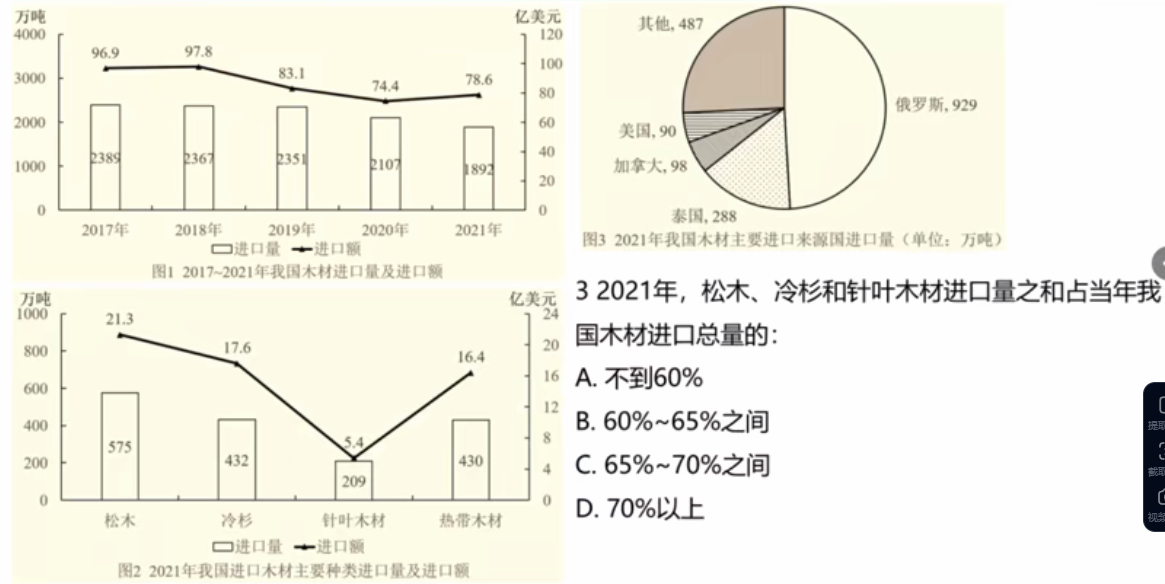
这个题选什么？
选B。要计算575+432+209，你会觉得要用高位叠加的方法，其实不用。就是随便估算一下就行。感觉575+432大概1000，加上209大概1200；然后总的看图1，为1892，用截位直除，为120/19=63，选B。7.2 基期比重
1、有关基期比重：
$\bigstar$认知过程：时间→ 一个→ 基期 → 关键词 → 占→ 基期比重
$\bigstar$公式：$基期比重=\frac{A}{B}\times\frac{1+b}{1+a}$，A和B都是现期，a和b是增长率
$\bigstar$方法与题型:
情况1：给现期比重，结合选项分析
情况2：不给现期比重。选项差距大，2位约分（什么意思？看例2(P175-P176)）；选项差距小，（1）看选项脸色：计算$\frac{A}{B}$的有效数字（至少算两三位，不能仅由$\frac{A}{B}$选出选项，会有较大误差），由后面的$\frac{1+b}{1+a}$大于1还是小于1，选出选项；（2）不看选项脸色：3位化1
2、对于博客1的“方法与题型”的情况2，发现选项差距大，则保留2位然后约分。这个方法怎么做呢？基期比重写为$\frac{3545}{15573.6}\times\frac{1+48.6\%}{1+109.8\%}$，计算时写为$\frac{35}{16}\times\frac{15}{21}$，16和15约掉，则剩下$\frac{35}{21}$，最终有效数字为1，选B。如果不好约分怎么办？那就选一个分数，算除法至少算2位有效数字，不能只算1位，然后相乘相除选出选项
3、对应博客1的“方法与题型”的情况2的例题：
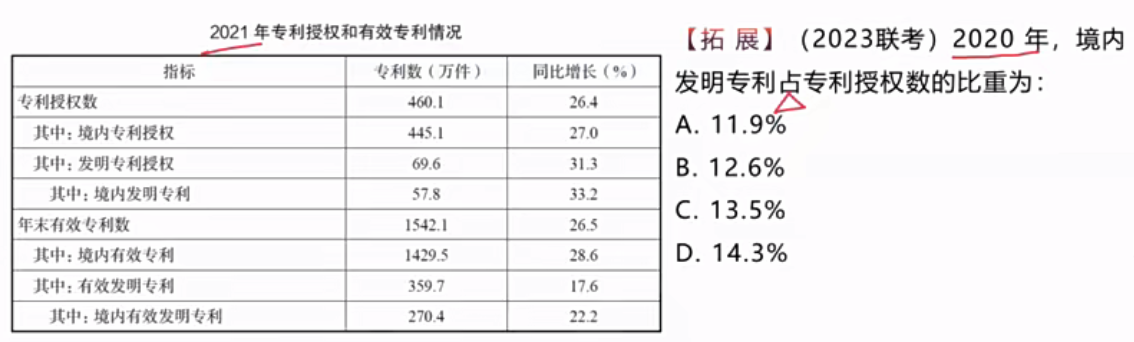
这个题是$\frac{57.8}{460.1}\times\frac{1+26.4\%}{1+33.2\%}$，我看$\frac{57.8}{460.1}$用截位直除，选项差距小，则为$\frac{5780}{460}$，大概是12.5%，然后$\frac{1+26.4\%}{1+33.2\%}<1$，那么就选A
而老师说，你这种方法要看选项的脸色，如果选项出现10.9%呢？和11.9%你选哪个？确实不好选
老师教了一个方法：等比修正，化1法
等比修正：3位列式，分子、分母原来多少倍，其加减的数字也要多少倍
化1：把$\frac{1+b}{1+a}$化1
对原式子$\frac{57.8}{460.1}\times\frac{1+26.4\%}{1+33.2\%}$三位列式后，为$\frac{578}{460}\times\frac{126}{133}$，然后用化1，即想把小尾巴$\frac{126}{133}$化为1，则用等比修正，为$\frac{578}{460}\times\frac{126}{133}=\frac{578}{133}\times\frac{126}{460}=\frac{578-4\times7}{133-7}\times\frac{126}{460}=\frac{550}{460}$，由于$\frac{578}{133}\approx4$，因此等比修正时$578-4\times7$。$\frac{550}{460}\approx11.9\%$，则选A
7.3 两期比重比较
1、题型1：两期比重比较
$\bigstar$认知过程：时间 → 两个 → 两期 → 关键词 → 占 → 两期比重 → 上升/下降（注意关键词哦！） → 两期比重比较
$\bigstar$例：与上一年相比，2021年前三季度分行业类别中，占全国 6.4 万家规模以上文化及相关产业企业营业总收入比重增加的行业个数是:
（问比重增加、且与上一年相比，则一定是现期比重和基期比重比较的，因此属于“两期比重比较”）
$\bigstar$方法：两期比重比较，看a(部分增长率)和b(总体增长率)大小，经验：占前a、占后b
a>b → 现期比重 > 基期比重 → 今年比重同比上升
a<b → 现期比重 < 基期比重 → 今年比重同比下降
a=b → 现期比重 = 基期比重 → 今年比重同比不变
$\bigstar$方法解释（方法需要解释是因为我一开始看不懂这个方法）：设部分的现期为A，部分增长率为a，总体的现期为B，总体增长率为b：
现期比重为$\frac{部分的现期}{总体的现期}=\frac{A}{B}$，即部分的现期比重；基期比重为$\frac{部分的基期}{总体的基期}=\frac{\frac{A}{1+a}}{\frac{B}{1+b}}=\frac{A}{B}\times\frac{1+b}{1+a}$，即部分的基期比重
两者对比，即只要对比$\frac{1+b}{1+a}$，即对比$a$与$b$的大小，即可知道部分的现期比重比部分的基期比重上升还是下降
2、 题型2：两期比重计算
$\bigstar$认知过程：时间 → 两个 → 两期 → 关键词 → 占 → 两期比重 → 上升/下降+ 百分点 → 两期比重计算，求比重的增长量
$\bigstar$例：与2021年相比，2022年我国移动数据流量业务收入在电信业务收入中的占比:
A.增加了约 3个百分点
B.减少了约 3个百分点
C.增加了约 13 个百分点
D.减少了约 13 个百分点
$\bigstar$公式：A和a为部分，B和b为总体，$两期比重差=\frac{A}{B}\times\frac{a-b}{1+a}$
$\bigstar$方法：口算”a-b”
（1）判升降：”a-b”结果为正，今年比重同比上升；结果为负，今年比重同比下降
（2）算多少：结果的绝对值<|a-b|。满足选项只有一个，当选；满足选项有多个，补全公式分析计算
解释：对于“算多少”，为什么“结果的绝对值<|a-b|”呢？
假设$a>0$，由于$|\frac{A}{B}\times\frac{a-b}{1+a}|=\frac{A}{B}\times\frac{|a-b|}{1+a}$，$\frac{A}{B}$是部分比整体，则一定是一个小于1的数，而1+a是一个大于1的数，因此$\frac{A}{B}\times\frac{|a-b|}{1+a}<|a-b|$成立
假设$a<0$，由于$1+a<1$，由于这是国家的报告，即某个值不会下降很多，即下降率$|a|$肯定很小，因此$1+a$使得$\frac{|a-b|}{1+a}$变大的幅度小于$\frac{A}{B}$使得$\frac{A}{B}\times|a-b|$变小的幅度，因此最终$a<0$时，$\frac{A}{B}\times\frac{|a-b|}{1+a}<|a-b|$还是成立
3、积累一下题型2“满足选项有多个”的计算技巧：
（1）关于例4(P177)，由于满足小于|a-b|的选项有多个，则要计算$\frac{A}{B}\times\frac{a-b}{1+a}$，题目中$\frac{A}{B}=0.408$，则$\frac{A}{B}\times\frac{a-b}{1+a}=0.4\times\frac{41.4}{1.4}$，$0.4\times41.4$的有效位数为16，$\frac{16}{1.4}$的有效位数应该是12，因此选B
（2）例3(P177)虽然不是“满足选项有多个”的题，但是可以计算，为$\frac{A}{B}\times\frac{a-b}{1+a}=0.4\times\frac{7.7}{1.003}$，还是根据（1）的计算方法，$0.4*7.7$的有效位数为3，$\frac{3}{1.003}\approx\frac{3}{1}$的有效位数肯定也是3，因此选B
（3）有坑题：选项的有效数字都相同怎么计算？
2017 年全国海洋生产总值 77611 亿元，比上年增长 6.9%，海洋生产总值占国内生产总值的9.4%。
2017 年，J省海洋生产总值为 7217 亿元，比上年增长 9.2%，海洋生产总值占地区生产总值的 8.4%。2017年，全省沿海沿江港口完成货物吞吐量 20.4 亿吨，同比增长 8.3%；集装箱吞吐量1698.8万标箱，同比增长5.5%。
(2020 山东)2017 年J省海洋生产总值占全国的比重比上年:
A.上升了约 0.2 个百分点
B.上升了约 2个百分点
C.下降了约 0.2 个百分点
D.下降了约 2 个百分点
这个题选什么？
选A。如何选出“选项的有效数字都相同”的正确选项？a=9.2%，b=6.9%，则a-b>0，排除CD。|a-b|=2.3%，则满足的选项有多个，需要计算。这个时候，你发现没，选项的有效数字都是2，则不能仅仅根据有效数字来选选项，还要根据小数点。$\frac{A}{B}=\frac{7217}{77611}\approx0.1$（差点以为$\frac{A}{B}=8.4\%$，真的太粗心了！），因此不能写为$\frac{A}{B}\times\frac{a-b}{1+a}=0.1\times\frac{2.3}{1.多}$，要写成$0.1\times\frac{0.023}{1.092}$，$0.1\times0.023=0.0023$，$\frac{0.0023}{1.092}\approx0.002=0.2\%$，则选A
8 平均数
1、平均数的识别
$\bigstar$关键词：均、每、单位面积、单位企业
$\bigstar$例题：
例：2021年，H省除Z市外其他地区的电子商务平台平均每个平台实现的交易金额约为多少亿元?
例：2016 年平均每所民办中等职业学校在校生人数约为:
例：2021年上半年，我国集成电路出口平均价格同比有所提高
$\bigstar$公式：
$现期平均数=\frac{A}{B}$
$基期平均数=\frac{A}{B}\times\frac{1+b}{1+a}$
$两期平均数的增长量=\frac{A}{B}\times\frac{a-b}{1+a}$
$两期平均数的增长率=\frac{a-b}{1+b}$
8.1 现期平均数
1、关于现期平均数
$\bigstar$识别：只出现一个时间，则求的现期
$\bigstar$题型：
（1）情况1：正常表述，后$\div$前
例：2024 年咱班有2000人，共收入6000亿，2024年班的人均收入为多少亿元
（2）情况2：倒装表述，单位的量做分子
例：该期间我国平均约多长时间新开一家海洋主题公园？
A.一个月 B.两个月C.三个月 D.四个月
（3）情况3：出现月均，日均的双重平均，优先除以时间（因为基本上$\div$时间更好计算，除以时间的时候不准估算），再平均（平均的时候再估算）
例：2024年咱班有2000人，共收入6000亿，2024年班的人均的月均收入为多少亿元？
$\bigstar$注意点：如果要除两个东西，先除第一个东西的时候不能估算，除以第二个东西的时候才能估算；如既要除以时间又要除以某个分母，优先除以时间的时候不能估算，除以那个分母的时候再估算
2、关于例2(P179)，我有话要说，就是这个题很坑，求每月，我啥也没看就除以12了，但是发现，它说的是“2021年上半年”，即应该除以6！！！要注意！！！
3、扩展题型：（作为情况4）求多个数的平均数
$\bigstar$方法：
（1）数据相差大，凑整加和，直除
例：2020-2024年，志哥的工资分别为1212元、596元、207元、780元、330元。2020-2024年，志哥的工资平均每年有多少元
怎么使用凑整加和呢？1212和596加起来约等于1800，207和780加起来约等于1000，还有个330，则为1800+1000+330=3130。有5年(2024-2020+1=5；前些天学的“年均增长量”，如果是2020-2024，则只有2024-2020=4年)；则3130/5=626
（2）数据相差小，削峰填谷
例：2020-2024年，志哥的工资分别为212元、196元、207元、180元、230元。2020-2024年，志哥的工资平均每年有多少元
怎么使用削峰填谷呢？找以上5个数字最接近的数字，比如我找200，则212对比200相差+12，196对比200相差-4，以此类推，能画出这个图：
削峰填谷这个思想用的很少，因为很鸡肋
$\bigstar$例题：
题1：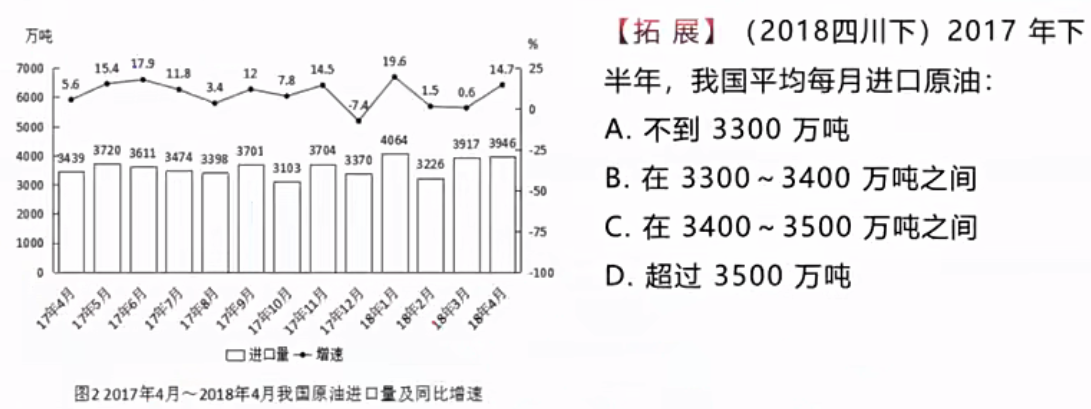
这个题选什么？
选C。下半年，说的是7月到12月。我一开始想用“削峰填谷”来写，但是计算峰和谷那些的差值太难了；我就用“凑整加和”了。3474+3398约是6800，3701+3103约是6800，3704+3370约是7000，加起来是20600，20600/6的有效数字是343，则选C。老师说可以用“削峰填谷”，但不是像那样求峰和谷的那些差值，而是使用“削峰填谷”的思想。图中是3474、3398、3701、3103、3704、3370这六个数字，怎么使用“削峰填谷”的思想呢？如果平均数为3500，则不可能，因为超过3500的只有2个数字；如果平均数是3300以下，也不可能，因为超过3300的有5个数字；则排除AD；如果平均数是3400，则可能，因为超过3400的有3个数字，没超过的有3个数字，因此选C。但是我觉得这个思想不够严谨，还是用“数据相差大，凑整加和，直除”的方法更好
8.2 基期平均数
1、题型1：先算出基期，再除以分母（这个是分母已知且固定的情况下，如除以月数量、日数量等；而题型2的分母由于需要通过$\frac{B}{1+b}$进行计算，才会衍生出公式$\frac{A}{B}\times\frac{1+b}{1+a}$），即
设A为现期，a为增长率，则基期为$\frac{A}{1+a}$，分母是x，则公式为$基期平均数=\frac{\frac{A}{1+a}}{x}$
方法：
（1）可以这么计算，即$平均数=\frac{A}{(1+a)\times x}$，即先计算$x_1=(1+a)\times x$，再计算$\frac{A}{x_1}$
（2）看$1+a$和$x$谁更好除，一般是$x$更好除，优先算$x_1=\frac{A}{x}$，再计算$\frac{x_1}{1+a}$
对应例题：例3(P180)
2、题型2：
$\bigstar$认知过程：时间→ 一个 → 基期 → 关键词 → 均 → 基期平均数
$\bigstar$公式：$基期平均数=\frac{A}{B}\times\frac{1+b}{1+a}$
$\bigstar$方法：选项差距大，2 位约分；选项差距小，3 位化 1
3、基期平均数的公式即$\frac{A}{B}\times\frac{1+b}{1+a}$的公式我有点看不懂，由例4(P180)来解释这个公式：
由题目问的，可以知道是$基期平均数=\frac{人数的基期}{多少所的基期}$，人数的增长率a=7.16%，多少所的增长率b=2.17%，就可以按照基期平均数的公式计算了
4、“公式$\frac{A}{B}\times\frac{1+b}{1+a}$怎么计算”的积累：
（1）如例4，为$\frac{197.33}{2069}\times\frac{1-2.17%}{1+7.16%}$，选项差距大，则$\frac{197.33}{2069}$截位直除，看成$\frac{197}{21}\approx93$，由$\frac{1-2.17%}{1+7.16%}<1$知道最后结果小于93，则选A不选B。要注意的是，如果只看$\frac{A}{B}$算出来第一位有效数字9，就很容易选B而错选，但是仅由$\frac{A}{B}$不看$\frac{1+b}{1+a}$得出选项，误差太大了，因此不可以这么做，还是要先算$\frac{A}{B}$（至少算两三位），然后看$\frac{1+b}{1+a}$大于1还是小于1选出选项才行。不过这种方法要看选项的脸色，万一选项里还有771，那么选871还是771呢？就不知道了
（2）例4有一个比较稳定的算法，即2位约分，$\frac{197.33}{2069}\times\frac{1-2.17%}{1+7.16%}=\frac{197.33}{2069}\times\frac{0.9783}{1.0716}$写成$\frac{20}{21}\times\frac{98}{11}$，然后估算，至少估算2位，$\frac{98}{11}=8.9$（肯定不到9），20和21可以直接约分，因此选A。如果不好约分怎么办？那就选一个分数，算除法至少算2位有效数字，不能只算1位，然后相乘相除选出选项
8.3 两期平均数
1、关于两期平均数比较：
$\bigstar$认知过程：时间 → 两个 → 两期 → 关键词 → 均 → 两期平均数 → 上升/下降 → 两期平均数比较
$\bigstar$例：2017年，S市服务业小微样本企业平均每万元营业收入缴纳营业税金及附加高于上年水平
$\bigstar$方法：两期平均数比较，看a(分子增长率)和b(分母增长率)大小，经验：后a、前b
a>b → 现期平均数 > 基期平均数 → 今年平均数同比上升
a<b → 现期平均数 < 基期平均数 → 今年平均数同比下降
a=b → 现期平均数 = 基期平均数 → 今年平均数同比不变
$\bigstar$方法解释（方法需要解释是因为我一开始看不懂这个方法）：
设平均数分子的现期为A，分子的增长率为a；分母的现期为B，分母的增长率为b，则
现期平均数为$\frac{A}{B}$，基期平均数为$\frac{\frac{A}{1+a}}{\frac{B}{1+b}}=\frac{A}{B}\times\frac{1+b}{1+a}$。能看出比较现期平均数和基期平均数，就是比较a和b的大小
2、关于两期平均数的增长量：
$\bigstar$认知过程：时间 → 两个 → 两期 → 关键词 → 均 → 两期平均数 → 上升/下降 +单位 → 平均数的增长量
$\bigstar$例：与 2018年相比，2019年全国商品房销售均价约:
A.增长 580 元
B.增长 710 元
C.下降 580 元
D.下降 710 元
$\bigstar$公式：$平均数的增长量=\frac{A}{B}\times\frac{a-b}{1+a}$
推导：$平均数的增长量=\frac{A}{B}-\frac{A}{B}\times\frac{1+b}{1+a}=\frac{A}{B}\times\frac{a-b}{1+a}$
$\bigstar$方法：一般选项差距大，2位列式，约分计算
$\bigstar$给个对应例题：
2019 年全国房地产开发投资132194亿元，比上年增长9.9%，增速比上年加快 0.4个百分点。其中，住宅投资 97071亿元，增长13.9%，增速比上年加快 0.5个百分点。2019年，全国商品房销售面积 171558 万平方米，比上年下降 0.1%。其中，住宅销售面积增长 1.5%，办公楼销售面积下降 14.7%，商业营业用房销售面积下降 15.0%。商品房销售额 159725 亿元，增长6.5%，增速比上年回落 5.7 个百分点。其中，住宅销售额增长 10.3% ，办公楼销售额下降15.1%，商业营业用房销售额下降16.5%。
(2020内蒙古)与 2018年相比，2019 年全国商品房销售均价约:
A.增长 580 元
B.增长 710 元
C.下降 580 元
D.下降 710 元
这个题选什么？
选A。为(159725/171558)*(6.5%-(-0.1%))/(1+6.5%)，2位列式，即(16/17)*(66/11)=16*6/17=56，选A。3、关于两期平均数的增长率：
$\bigstar$认知过程：时间 → 两个 → 两期 → 关键词 → 均 → 两期平均数 → 上升/下降+%→ 平均数的增长率
$\bigstar$例：2018 年前三季度，平均每万元社会物流总额产生的物流费用比上年同期:
A.上升了不到 1%
B.上升了 1% 以上
C.下降了不到 1%
D.下降了 1% 以上
$\bigstar$公式：$平均数的增长率=\frac{a-b}{1+b}$
$\bigstar$方法：口算”a-b”
判升降：结果为正，今年平均数同比上升；结果为负，今年平均数同比下降
算多少：看b符号，即
（1）若b>0，则1+b>1，那么平均数的增长率的绝对值<|a-b|（如例3(P181)就用到了这点）
（2）若b<0，则1+b<1，那么结果绝对值>|a-b|
4、补充两题：
题1：
这个题选什么？
选D。a=5.7%,b=-8.2%，则a-b=13.9%>0，排除AB。1+b<1，则最终增长率>13.9%成立。选D题2：
这个题选什么？
选C。a=-0.8%,b=-0.3%，则a-b=-0.5%<0，排除AB。1+b<1，则最终增长率>0.5%成立。且1+b离1非常进，因此结果肯定很接近0.5%，因此是C不是D。9 倍数
9.1 现期倍数
1、关于倍数
$\bigstar$关键词(倍)：A是B的几倍、A 比B多几倍、A 超过 B的几倍
例：2021 年广东农林牧渔业总产值约为9年前的多少倍?
例：按经营单位所在地分，2023 年一季度，城镇消费品零售额约比乡村消费品零售额多多少倍?
例：2017年，全国处理的支付交易类钓鱼网站数量超过金融证券类钓鱼网站2倍的月份有几个?
$\bigstar$求倍数，找分割词，看问法
常见分割词：是、与、为、比、超过
A是/为B的几倍 → $\frac{A}{B}$ 例：A=500、B=100，A是B的多少倍？
A与B的比例 → $\frac{A}{B}$ 例：A=500、B=100，A与B的比例为？5:1
A比B多几倍（多几倍就是多多少增长率） → $\frac{A-B}{B}=\frac{A}{B}-1$ 例：A=500、B=100，A比B多多少倍？多(500-100)/100=4倍
A超过B的N倍 → A>B$\times$N 例：A=490、B=100，A是否超过B的4倍？
2、倍数的补充例题：
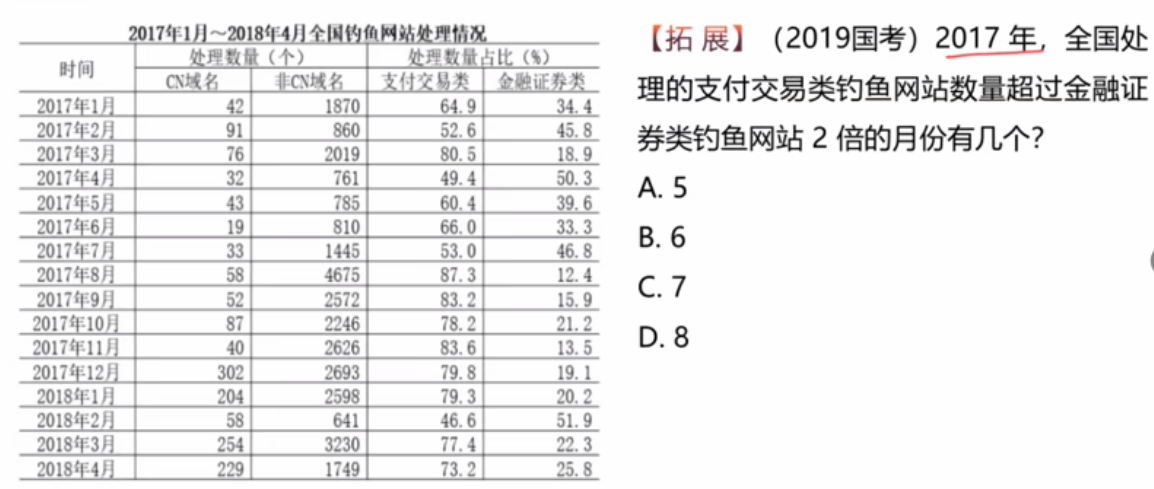
这个题选什么？
选B。这题是拿比重（即图中说的“占比”）看倍数关系，是3月、8月-12月。有个同学有个思考，说A超过B的2倍，则直接看A的占比是否大于66.7%就行。这样行吗？不行。因为不能保证A+B=100%
9.2 基期倍数
1、关于基期倍数
$\bigstar$认知过程：时间 → 1个 → 基期 → 关键词 → 倍 → 基期倍数
$\bigstar$公式：$基期倍数=\frac{A}{B}\times\frac{1+b}{1+a}$
$\bigstar$方法：选项差距大，2位约分
选项差距小，3 位化 1
2、对于例4(P185)，我有话要说！
这题无法代入公式$\frac{A}{B}\times\frac{1+b}{1+a}$，因为没给a和b，给的是两期比重的增长量（百分点数据）（我这个没心眼的，居然直接代入了）
给的2020年东部地区的比重为39.93%，说比2010年东部地区的比重多2.15个百分点，则2010年东部地区的比重为39.93-2.15=37.8%
给的2020年东北地区的比重为6.98%，说比2010年东北地区的比重少1.2个百分点，则2010年东部地区的比重为6.98+1.2=8.1%
则直接东部地区的基期比东北地区的基期，为$\frac{37.8}{8.1}\approx\frac{37}{8}\approx4.6$
9.3 平均数倍数
1、关于平均数的倍数
$\bigstar$认知过程：时间 → 1个 → 现期 → 关键词 → 倍 → 现期倍数 → 主体 → 平均数 → 平均数的倍数
$\bigstar$公式：$平均数的倍数 =\frac{A}{B}\div\frac{C}{D}=\frac{A\div C}{B\div D}$
$\bigstar$方法：
第一步：弄清分子、分母(后÷前)
第二步：口算分子倍数，口算分母倍数，$平均数的倍数=\frac{分子的倍数}{分母的倍数}$
$\bigstar$注意点：有时候直接告诉了你分子的倍数和分母的倍数，如告诉你某些比重（占比），你就不用算了，如题1
$\bigstar$补充例题：
题1：
这个题作为方法的讲解：这是现期平均数的倍数
（1）方法1：代入公式，为$\frac{10.75}{2060}\div \frac{43.69}{17581}=\frac{10.75\div 43.69}{2060\div 17581}$，分子的倍数为$\frac{107}{44}$（选项差距大，截位直除分子3位，分母保留2位），有效数字是25，分母的倍数为$\frac{206}{18}$，有效位数是11，则$平均数的倍数=\frac{分子的倍数}{分母的倍数}=\frac{25}{11}\approx2$，选D
（2）方法2：因为直接告诉了你占比。因此直接知道分子倍数为24.6%，分母倍数为11.7%，则为2倍差不多，选D
10 间隔增长
10.1 间隔增长率（最近几年考出花来了，热度高）
10.1.1 正向考法
1、关于间隔增长率（正向考法）
$\bigstar$认知过程：时间 → 两个 → 两期 → 关键词 → 増长 + % → 増长率 → 隔一年 → 间隔增长率
与同比不同，同比是2024年与2023年比较，而间隔增长率是2024年与2022年比较，中间间隔了一年
$\bigstar$例：2024 年床位数仍然比2022年增加了多少%？
$\bigstar$公式：
求2024年比2022年的间隔增长率$r$，则设2024年的同比增长率为$r1$，2023年（不是2022年哦！）的同比增长率为$r2$
则公式为$间隔增长率r=r_1+r_2+r_1\times r_2$（记忆口诀：和$+$积）
例：2024 年志哥工资的同比增长率为10%，2023年同比增长率为10%，则2024 年志哥工资比2022 年增长多少%
例：2024年志哥工资的同比增速为10%，增长率比上年降低10个百分点，则2024 年志哥工资比2022 年增长多少%
$\bigstar$速算：
先算加和(占间隔增长率的大头)，快速计算 → 计算$r1+r2$或者计算$2\times r1±百分点$（百分点是$r2-r1$，即上年比今年多的百分点），观察选项，是否唯一
不唯一，再算乘积(占间隔增长率的小头)，大致估算即可，百化分或参照法
不唯一算乘积的时候，百化分也行，但是老师推荐使用乘积参照法：
计算$10\%\times10\%$时，不看两个百分号，直接$10\times10$，计算的时候加上一个%，还差一个百分号，就除以100，即原式=$\frac{10\times10}{100}\%=1\%$
即$a\%\times b\%$不看2个百分号的a与b乘积对应最终结果的百分数为：
可知，若$a\times b<100$，则$a\%\times b\%<1\%$，则$a\%\times b\%$可忽略，可以不用计算
注意，计算$a\times b$乘积，可以用“2.6 乘法速算”来计算
2、对于例1(P186)，可以作为模板题，交我们用方法，$r_1+r_2=11.9\%$，排除BD。$r_1\times r_2$去掉百分号的$5.6\times6.3<100$，即可忽略不计，说明最终结果与11.9%很接近，相差不到1%(因为$5.6\times6.3<100$)，则选12.26%，不选13.21%
10.1.2 逆向考法
1、关于间隔增长率 (逆向考法)
$\bigstar$认知过程：时间 → 两、三个 → 关键词 → 增长率 → 给现期 $r_1$ 与间隔$r$ → 求基期增长率 $r_2$
$\bigstar$公式：
设2022年比2020年的增长率为$r$，2022年同比增长为$r_1$，则2021年同比增长率为$r_2=\frac{r-r_1}{1+r_1}$（由公式$r=r_1+r_2+r_1\times r_2$推导出，很好推导）。若$r-r_1>0$，则$r_2>0$；若$r-r_1<0$，则$r_2<0$
$\bigstar$例：2024 年志哥工资的同比增长率为10%，比2022年同比增长率为15%。则2023年志哥工资比 2022 年增长多少%
例：2024年志哥工资的同比增速为10%，两年平均增长12%。则2023 年志哥工资比 2022 年增长多少%
$\bigstar$考法：（以上例题的两种考法这两年考得特别多！！！）
（1）考法1：给$r$和$r_1$，求$r_2$。直接代入公式$r_2=\frac{r-r_1}{1+r_1}$即可
（2）考法2：给年均增长率$r_平$和$r_1$，求$r_2$。推导如下：
什么是年均增长率（此时还没讲），即设2026年现期为A，2024年的为C。设两年平均增长率为$r_平$，则$C(1+r_平)^2=A$
则$\frac{A}{C}=(1+r_平)^2=r_平^2+2r_平+1$，即$\frac{A}{C}=r_平^2+2r_平+1$成立，则$\frac{A}{C}-1=r_平^2+2r_平$，而$\frac{A}{C}-1$就是间隔增长率
即间隔增长率$r$和两年平均增长率$r_平$的关系是$r=r_平^2+2r_平$，写成$r=r_平+r_平+r_平^2$可能更好算一点（注意，计算这个的时候，遵循“间隔增长率（正向考法）”公式的速算原则！！！记得用乘积参照法！！！）
求出$r$后，由$r$和$r_1$直接代入公式$r_2=\frac{r-r_1}{1+r_1}$求$r_2$
$\bigstar$例题：
（1）题1：
2021 年，全国纺织品服装出口3155 亿美元，同比增长 8.4%。其中，纺织品出口 1452.2 亿美元，同比下降 5.6%，较2019年增长 22.0%；服装出口 1702.8 亿美元，同比增长 24.0%，较 2019年增长16.0%。其中，针织服装及衣着附件出口864.8 亿美元，同比增长 39.0%;织服装及衣着附件出口 701.2亿美元，同比增长12.6%。
(2023国考)2020年，全国服装出口额比2019年
A.增长了 10% 以上
B.下降了 10% 以上
C.增长了不到 10%
D.下降了不到 10%
这个题选什么？
选D。我一开始看错了，我以为r1-r间=16%。而这题是r1=24%，r间=16%，则结果为(16%-24%)/(1+24%)=-6%，选D。（2）题2：（非常重要，告诉了我们算$r=r_平+r_平+r_平^2$的速算技巧！！！）
2021 年上半年，S市工业战略性新兴产业总产值7164.68亿元，比去年同期增长19.6%，两年平均增长 12.3%。其中，新能源汽车、新能源和高端装备产值同比分别增长 2.5 倍、32.1%和24.5%。
(2023国考)2020年上半年，S市工业战略性新兴产业总产值同比增长在以下哪个范围内?
A.不到 7%
B.7~10%
C.10~13%
D.超过13%
这个题选什么？
选A。r=r平+r平+r平*r平=12.3%+12.3%+12.3%*12.3%，由于12.3%+12.3%约等于24%左右，12.3*12.3在一百多，根据乘积参照法应该是1%，则r大概是25%左右。则r2=(r-r1)/(1+r1)=(25%-19.6%)/(1+19.6%)，截位直除为54/12，有效数字为4，即4%左右，则选A。（3）题3：
2021年1~2月，全国网上零售额17587 亿元，同比增长 32.5%，两年平均增长 13.3%。其中，实物商品网上零售额 14412 亿元，同比增长 30.6%，两年平均增长 16.0%，占社会消费品零售总额的比重为 20.7%；在实物商品网上零售额中，吃类、穿类和用类商品分别增长 41.6%、44.3%和25.1%，两年平均分别增长 33.8%、8.7%和16.0%。
(2024四川下)2020年1~2月，将吃类、穿类和用类商品的实物商品网上零售额同比增速从高到低排列，下列排序正确的是:
A.吃类、用类、穿类
B.吃类、穿类、用类
C.穿类、吃类、用类
D.穿类、用类、吃类
老师带着做：计算$r_2$还要从高到低排序，这也太麻烦了；但是你看“穿类”，能看一看（$r_平+r_平\approx16\%$，$r_平\times r_平\approx不到1\%$，则$r$大概为17%）看出$r
注意，我记得有一题也和这题一样，不用算全部的，只要求最大或者最小就可以锁定选项！真方便啊！
10.2 间隔倍数
1、关于间隔倍数
$\bigstar$认知过程：时间 → 两个 → 两期 → 关键词 → 倍 → 倍数 → 隔一年 → 间隔倍数
$\bigstar$例：2017年上半年约是2015年上半年的多少倍
A.1.3 B.1.4 C.1.5 D.1.6
$\bigstar$方法：
第一步：根据选项，推出间隔增长率 → 是几倍-1=间隔增长率，多几倍 = 间隔增长率
第二步：估算间隔增长率
反正本质还是考“间隔增长率（正向考法）”
$\bigstar$例题：
题1：
2017 年上半年医药工业规模以上企业实现主营业务收入15314.40 亿元，同比增长 12.39%，增速较上年同期提高 2.25 个百分点。各子行业中，增长最快的是中药饮片加工，化学药品制剂、中成药、制药设备的增速低于行业平均水平。
(2017新疆)在医药工业规模以上企业实现主营业务收入上，2017年上半年约是 2015 年上半年的()
A. 1.13 倍
B. 0.13 倍
C. 1.24 倍
D. 0.24 倍
这个题选什么？
选C。r1=12.39%，r2=r1-2.25%=10.14%，则r>20%，则倍数>1.2，选C。10.3 间隔基期
1、关于间隔基期
$\bigstar$认知过程：时间→ 一个 → 基期 → 隔一年 → 间隔基期
$\bigstar$例：2024年志哥工资有100元，同比增长10%，2023年同比增长20%。则2022 年志哥工资为多少元
$\bigstar$方法：
公式：设2024年现期为A，2024比2022年的增长率为r，则算2022年的间隔基期，$间隔基期=\frac{A}{1+r}$
第一步：先估算间隔增长率$r$。选项差距大，估算到十位；选项差距小，估算到个位
第二步：厂除求基期
$\bigstar$例题：（作为模板题，教我们理解怎么速算）
按常住地分，2015 年城镇居民人均可支配收入31195元，比上年增长 8.2%，增长率比 2014 年下降 0.8 个百分点。
(2015江苏)2013 年，城镇居民人均可支配收入约为多少万元?
A. 1.9
B. 2.2
C. 2.6
D. 3
这个题选什么？
选C。r1=8.2%，r2=8.2+0.8=9%，r=r1+r2+r1*r2=17.2%+不到1%（不到1%是使用了乘积参照法），因为选项差距大，只需要看间隔增长率的十位数，则倍数约为1.2，用截位直除，为311/12，约为25，选C。10.4 间隔增长量（不常考）
1、关于间隔增长量
$\bigstar$认知过程：时间 → 两个 → 两期 → 关键词 → 增长 + 单位 → 增长量 → 隔一年 → 间隔增长量
$\bigstar$例：2024 年志哥工资有100元，同比增长10%，2023年同比增长20%，2024年志哥工资比2022年增长多少元
$\bigstar$方法：
与“5 增长量的题型3：给现期、增长率求增长量”的计算方法类似，设2024年现期为A，间期增长率为$r$，2022年的为C，则$间期增长量=C\times r=\frac{A}{1+r}\times r$，将间期增长率$r$百化分，为$|r|=\frac{1}{N}$，则$间期增长量=\frac{A}{1+r}\times r=\frac{A}{1+\frac{1}{N}}\times \frac{1}{N}=\frac{A}{N+1}$，即最终公式为$间隔增长量=\frac{A}{N+1}$
第一步：求间隔增长率$r$
第二步：百化分，$|r|=\frac{1}{N}$算出$N$，按公式求间隔增长量
11 乘积增长率
1、关于乘积增长率
$\bigstar$认知过程：增长率计算→数据不全→ 间接→ $A=B\times C$ → 乘积增长率
$\bigstar$题目中说了$A=B\times C$，如部分=整体$\times$比重，总额=单价$\times$数量，面积=长$\times$宽等；则A的增长率和B和C的增长率的关系：$r_A=r_B+r_C+r_B\times r_C$
$\bigstar$速算：参照间隔增长率
$\bigstar$例题：
题1：（作为乘积增长率的模板题）
总出口额=数量$\times$单价，则设总出口额的增长率为$r$，数量的增长率为$r_1$，单价的增长率为$r_2$，则$r=r_1+r_2+r_1\times r_2$，$r_1=2.8\%$，$r_2=\frac{4.9-4.5}{4.5}=8.8\%$，则$r=11.6\%+\frac{2.8\times8.8}{100}\%$，接近12%，选A
题2：（我没写出来，这题挺难想到的）
这个题选什么？
选C。下面的柱状图的图例写着“我国海洋第三产业增加值占海洋生产总值占比”可以知道，海洋第三产业增加值=海洋生产总值*比重，而现在在算增加值的增长率，即它也是一个乘积增长率，r1=6.2%，r2=(60-59.1)/59.1=1.5%，r=r1+r2+r1*r2=6.2%+1.5%+(6.2*1.5)/100%，大概是7.7%，即选C。12 年均增长率
1、关于年均增长率
$\bigstar$认知过程：时间 → 时间段 → 关键词 → (年均) +增长 +% → 年均增长率年均增长最快/慢
$\bigstar$例：2024年志哥工资为100元，2021年为80元。2021-2024年，志哥工资的年均增长多少%
$\bigstar$公式：$基期\times(1+年均增长率)^{增长次数}=现期$，即$(1+年均增长率)^{增长次数}=\frac{现期}{基期}$
增长次数在之前有讲过怎么算
12.1 年均增长率比较
1、关于年均增长率比较
$\bigstar$公式：$(1+年均增长率)^{增长次数}=\frac{现期}{基期}$
$\bigstar$方法：现期年份差(增长次数)相同，直接比较$\frac{现期}{基期}$，结果(总增长率)大，年均增长率大
$\bigstar$例：2024 年志哥与郭子的工资分别为100元、80元，2022年分别为50元、20元。2022-2024年，谁的工资的年均增长率大
$\bigstar$扩展例题：
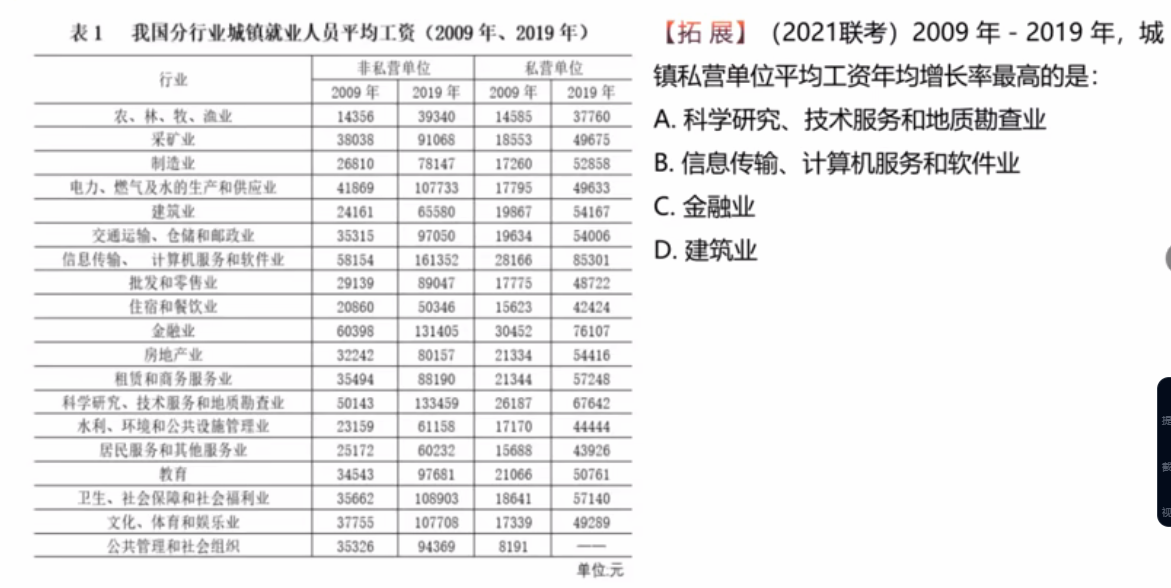
这个题选什么？
选B。就是比较现期/基期的大小。发现只有B才是3开头的，因此B最大。12.2 年均增长率计算（很少考）
1、关于年均增长率计算
$\bigstar$公式：$(1+年均增长率)^{增长次数}=\frac{现期}{基期}$
$\bigstar$方法：
选项大部分在10%以上，还有其他方法，多用于省考
2、用例3(P189)作为例题，解释计算年均增长率的方法“居中代入”怎么用
$\frac{现期}{基期}=\frac{104.24}{61.68}$，用截位直除，为$\frac{104}{62}\approx1.7$，这一题增长次数为2，则公式为$(1+r)^{2}=1.7$
因为选项大部分在10%以上，这一题可以用居中代入
代入B，$(1+0.3)^2=1.69$，和1.7接近，则选B
13 混合增长率
1、关于混合增长率
$\bigstar$认知过程：增长率计算→数据不全→ 间接去求 → 有A=B+C的混合关系 → 混合增长率
$\bigstar$混合关系：
（1）判定混合关系：
补充一下，当出口>进口时，顺差=出口-进口；当进口>出口时，逆差=进口-出口
（2）还能这样判定混合关系：
例如题目中说2018年H市完成邮电业务总量108.2亿元。其中，邮政业务总量40.8亿元，同比增加26.5%；电信业务总量67.4亿元，同比增加56.7%。
由关键词“其中”，可以判定混合关系为邮电业务总量=邮政业务总量+电信业务总量
$\bigstar$做题识别：
（1）现期、基期、增长量，任给其二，可直接计算增长率
（2）只给现期，优先考虑是否考查混合增长率（要看里面是否有混合的关系）
$\bigstar$方法解析：确定范围
① 居中不中。解释：设有A=B+C的混合关系，若B的增长率为10%，C的增长率为20%，则全班的混合增长率$r$的范围是居中的，即$10\%<r<20\%$
② 偏向基期量大的一方。解释：如果B基期为100，C基期为10，则混合增长率$r$和B的增长率10%更靠近
③ 只累计不滑坡，当月就比当月累计多
④ 线段法计算：计算数值（具体怎么计算在下面的“做题题型”里），距离与量成反比
⑤ 三角杀（没学，“牟”视频学一下）
$\bigstar$做题题型：
（1）题型1：求混合增长率
第一步：找居中位置。即设有A=B+C的混合关系，若B的增长率为10%，C的增长率为20%，则全班的混合增长率$r$的范围是居中的，即$10\%<r<20\%$，设它此时为15%
第二步：看谁基期（千万不能看现期）大。（基期有可能没给，需要根据现期和增长率进行计算）若B的基期大，则$10\%<r<15\%$；若C的基期大，则$15\%<r<20\%$
（2）题型2：求部分增长率
找大致范围。即设有A=B+C的混合关系，若A的增长率（即混合增长率）为17%，B的增长率为10%，求C的增长率。由于10%<17%，则10%<17%<C的增长率；
若A的增长率（即混合增长率）为17%，B的增长率为25%，求C的增长率。由于17%<25%，则C的增长率<17%<25%；
还有一种特殊情况，若A的增长率（即混合增长率）为-12.3%，B的增长率为-10.8%，求C的增长率。由于-12.3%<-10.8%（即不能忽略负号！！！），则C的增长率<-12.3%<-10.8%
（3）题型3：题型1和题型2的方法都不足以求混合增长率和部分增长率怎么办？
那使用线段法。
操作：画一条线段，部分写两边，混合写中间，条件标上去
结论：距离与量成反比
距离 → 部分增长率与混合增长率的差
量 → 部分的基期量(一般拿现期估算)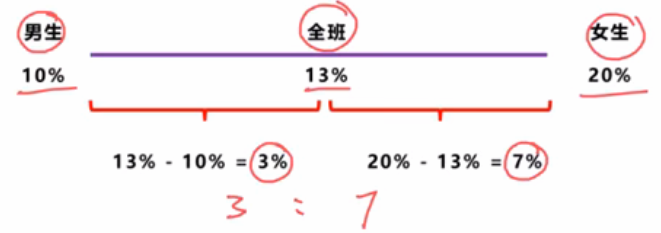
距离的比是3:7，那么可以得出量的比是7:3，即距离和量成反比
2、积累一下做题步骤：
（1）例1(P189)。混合关系为进出口=进口+出口，现在要求混合增长率。先找居中位置，即可知13.4%<r<14.3%，由这一个就能选出C
（2）例4(P191)。混合关系为邮电业务总量=邮政业务总量+电信业务总量，现在要求混合增长率。先找居中位置，可知26.5%<r<56.7%，居中位置大概是41%；只能排除CD。再看谁的基期大，即看$\frac{40.8}{1+26.5\%}$和$\frac{67.4}{1+56.7\%}$的大小比较，发现电信业务总量的基期大，则最终41%<r<56.7%，则选B
3、扩展一个求“混合增长率”的题：
题1：
2016 年女性参加生育保险的人数达8020万人，比2010年增长 49%。2016年参加城镇职工基本医疗保险的女性 1.4 亿人，比2011年增长 21.5%；参加城镇居民基本医疗保险的女性1.9 亿人，比2011年增长了1.5 倍。
(2021北京)2016 年参加城镇职工和城镇居民基本医疗保险的女性比 2011年增长了约多少倍?
A. 0.7
B. 1.2
C. 1.7
D. 2.2
这个题选什么？
选A。这题的混合关系是城镇职工和城镇居民基本医疗保险的女性=城镇职工基本医疗保险的女性+城镇居民基本医疗保险的女性。注意，增长了1.5倍，即增长率为150%。先确定居中位置。21.5%< r<150%。居中位置假设为85%。排除CD。
城镇职工基期为1.4/(1+21.5%)，城镇居民为1.9/(1+150%)，基期是城镇职工大，则21.5% < r<85%。选A。
这一题我忘了注意这个点，就是“多了多少倍”、“增长了多少倍”的意思都是增长率的意思，如增长1.5倍，即增长率为150%。
4、扩展一个求“部分增长率”的题：
题1：
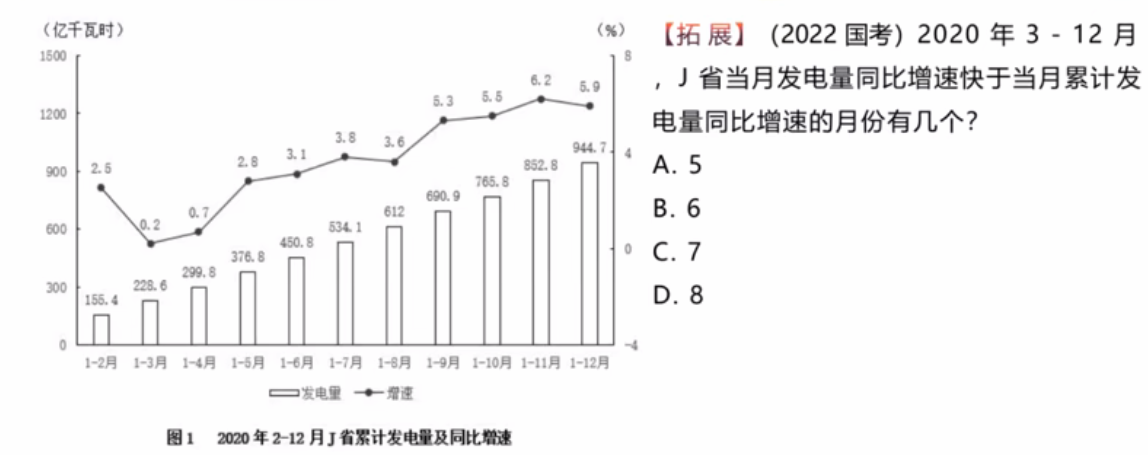
这个题选什么？
选C。拿3月举例子，3月当月发电量同比增速，和当月累计发电量（即1-3月累计发电量）同比增速比较，因此我们要计算3月当月发电量同比增速。3月+1-2月=1-3月，则1-3月为混合增长率，其他是部分增长率，则这一题求的是部分增长率。则3月增长率<0.2%<2.5%。因此3月当月发电量同比增速没有快于当月累计发电量同比增速。
以此类推，4、5、6、7、9、10、11月都满足要求，因此有7个月份，选C。
题2：
这个题选什么？
选C。这题的混合关系是什么？发现柴油机累计销量+汽油机累计销量=全国内燃机累计销量，因此混合关系是柴油+汽油=全国内燃机。因此让我们求部分增长率。
则很容易得到r<4.11%<13.04%，排除D。
然后就只能用线段法：
14 综合分析
1、做题逻辑：
注意一下以上图的细节：
（1）反超：之前我没有超过你，今年我超过你了，这是反超
（2）首超：是首次超过
（3）“是几倍”是$\frac{A}{B}$，而“多几倍”是增长率，即$\frac{A}{B}-1$
（4）直接判断“均”等字眼错，是有前提的。看它带的感情色彩，如我说公积金实缴额均超过2000亿元，公积金是积极的感情色彩，说“均”，不能直接判定它直接错；又如看不出感情色彩的句子带“均”，就有可能错，只是不看，但是后续如果选不出来还是要计算这个带“均”的选项的！
$\bigstar$补充一个：“最”字不算“错”的概率大！！！
2、补充习题：
$\bigstar$在这之前，记住一句话！两期比例比较为正确答案的概率相对较高！换句话说，优先关注两期比例比较的选项！
$\bigstar$记住！优先算好算的！难算的可以先跳过！！！如现期、基期、增长量好算的程度大于增长率，可以优先算这些选项！！！
$\bigstar$有时候题干会问“以下哪个选项是错的”！别被坑了！
题1：（特别注意B，B差点弄错）
这个题选什么？
选D。A是19，9%-0.4%=19.5%，A错；对于B，发明专利占66%，非发明专利占34%，“高一倍”代表增长率=100%，增长率=(66-34)/34<100%，因此B错；
对于C，实现利润197.6亿元，比上年增长一倍，即基期=197.6/(1+100%)<100，因此C错；
对于D，考点是“两期比重对比”，a=5%，b=13.7%，a < b，则现期比重<基期比重，D对。
题2：
这个题选什么？
选B。对于A，对比1393.4/(1+228.5%)与1412.4/(1-5.4%)，一看就是后面大，则A错。对于B，a=46.3%，b=16.6%，a>b，则B对。
对于C，27.65/365=0.08万人次，C错。
对于D，给现期、增长率求增长量。用公式：增长量=现期/(N+1)，r=5.5%，则N=18，增长量=1698.8/(18+1) < 100，则D错。
题3：
2022年1~7月，全国规模以上工业发电4.77万亿千瓦时，同比增长1.4%，增速比上半年加快0.7个百分点。7月份，全国发电量8059亿千瓦时，同比增长4.5%，增速比上月加快3.0个百分点。分品种看，7月份火电由降转增，同比增长5.3%；由于来水偏枯，水电同比增长2.4%，增速比上月放缓26.6个百分点；风电同比增长5.7%，增速比上月放缓11.0个百分点；核电同比下降3.3%，降幅比上月收窄5.7个百分点；太阳能发电同比增长13.0%，增速比上月加快3.1个百分点。
2022年1~7月，全社会用电量累计49303亿千瓦时，同比增长3.4%。分产业看，第一产业用电量634亿千瓦时，同比增长11.1%；第二产业用电量32552亿千瓦时，同比增长1.1%；第三产业用电量8531亿千瓦时，同比增长4.6%；城乡居民生活用电量7586亿千瓦时，同比增长12.5%。7月份，全社会用电量8324亿千瓦时，同比增长6.3%。分产业看，第一产业用电量121亿千瓦时，同比增长14.3%；第二产业用电量5132亿干瓦时，同比下降0.1%；第三产业用电量1591亿千瓦时，同比增长11.5%；城乡居民生活用电量1480亿千瓦时，同比增长26.8%。
(扩展题)能够从从上述资料中推出的是:
A.2022年7月全国太阳能发电增长量最大
B.2022年6月全国核电发电量比5月份高
C.2022年7月第二产业用电量高于上半年第二产业月均用电量
D.2021年7月第一产业用电量低于2021年上半年第一产业月均用电量
这个题选什么？
选C。对于A，没讲对应基期，因此未知。对于B，降幅是绝对值，即降幅为3.3%+5.7%=9%，即增速为-9%，则6月小于5月，B错。
对于C，2022年7月第二产业用电量为5132，上半年第二产业月均用电量=32552/7=4开头的数，则C对。
D懒得算了，反正错的。
题4：
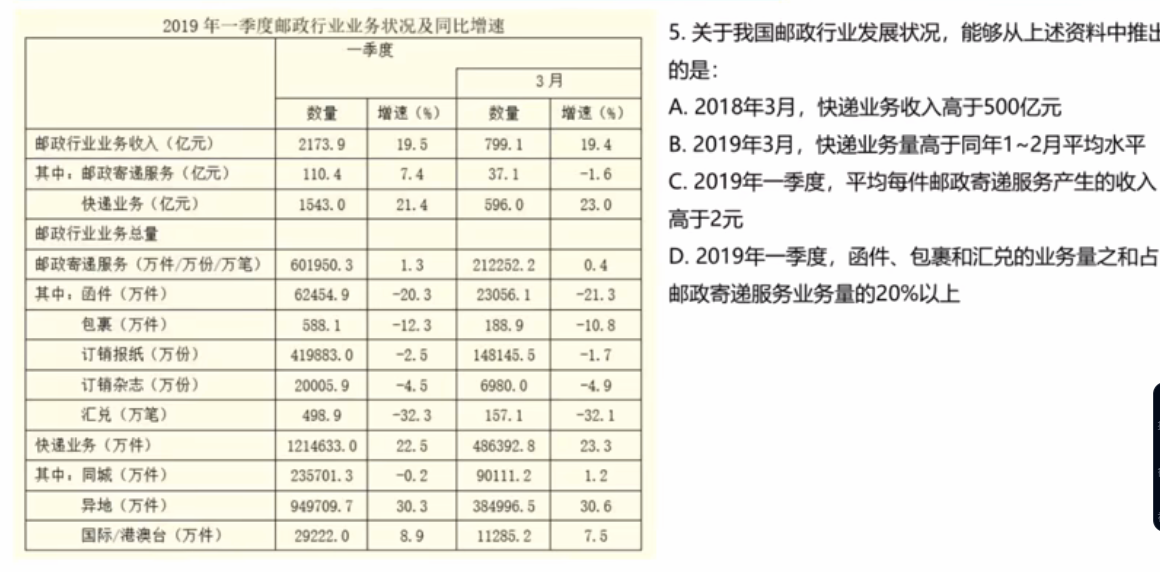
这个题选什么？
选B。对于A，596/(1+23%)，截位直除为596/12=4开头的数，则A错
对于B，老师的这种写法要记住：
3月和1-2月平均水平相比，就是在比较3月$\times$3和1-3月，即486392$\times$3与1214633进行比较，确实比它大，B对
写出B对后，CD忽略
题5：
这个题选什么？
选B。之前讲过带“均”字的选项容易是错的。B中，(3660-3057)/3057=603/3057，截位直除为603/31=1开头的数，则B错，选B。题6：
这个题选什么？
选D。由常识，东北地区的房价肯定同比增长最小。不敢选，但是好像必须得这样，因为怕做不完题！题7：
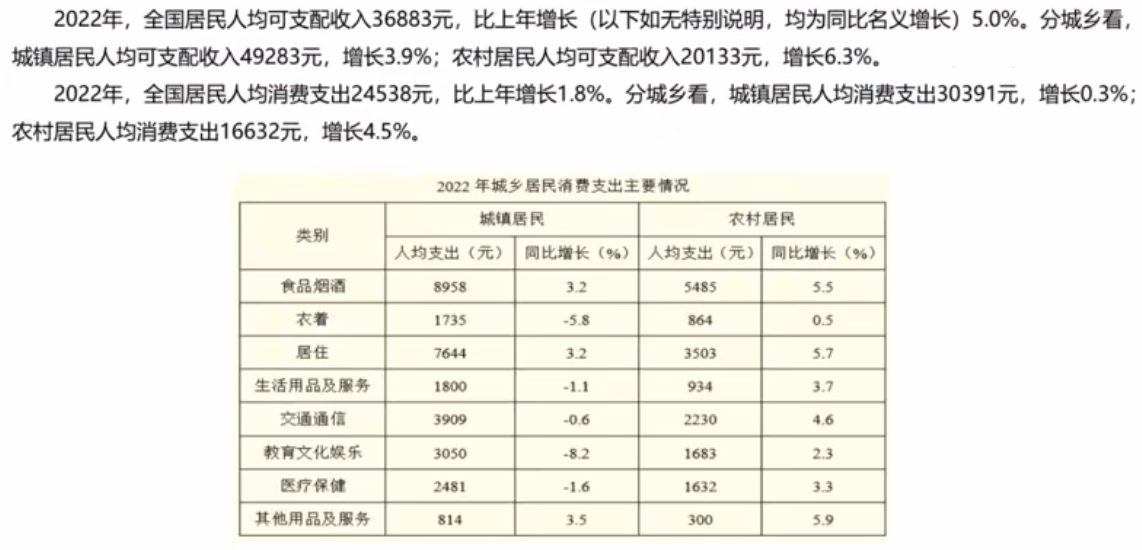
8.根据资料，下列说法正确的是()。
A.2022年，农村居民人均可支配收入较去年增加上千元
B.2021年，全国居民人均消费支出首次超过了2.4万元
C.与2021年相比，2022年城镇居民在衣着上的消费支出减少最多
D.2021年，无论在城镇还是农村，居民消费支出的重点都是食品烟酒支出和医疗保健支出
这个题选什么？
选A。D的“无论，都”让我怀疑它是错的，先不看。B的“首超”让我怀疑它是错的，先不看。看AC。A中，6.3%=1/16，N=16，则增长量=20133/(16+1)=一千多，A对。
题8：
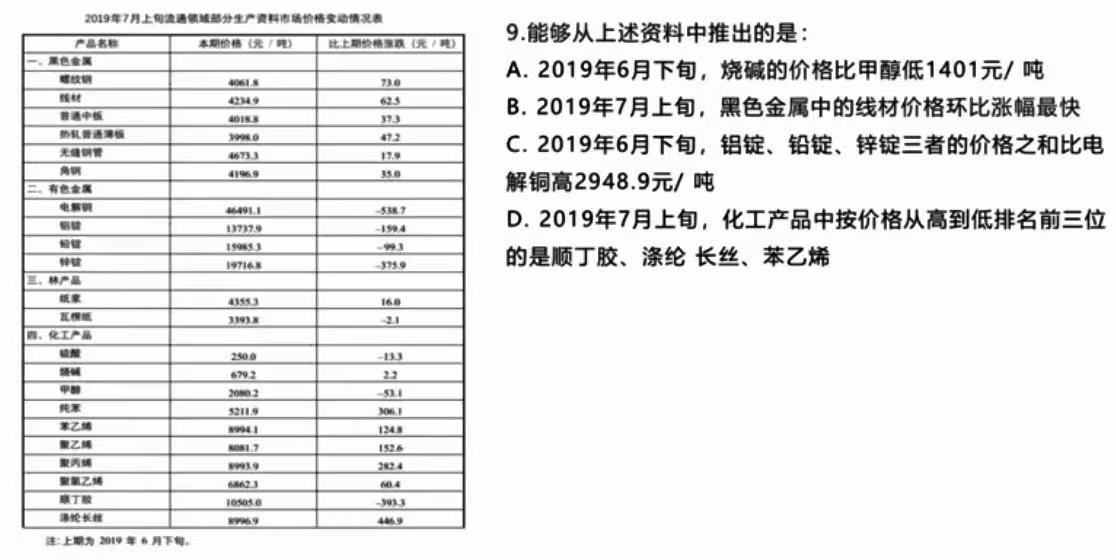
这个题选什么？
选D。A通过计算发现差值为1456.3，错误。B就是按照公式：增长率=增长量/基期，有点难算，先跳过。
C也有点难算，先跳过。
D直接就是现期排序，很简单，发现是对的，选D。
题9：
这个题选什么？
选D。A直接能看出来错误。B看斜率，是错误的。
C是15300/365=4开头的，C错。
D直接就是眼睛算增长量，很简单，是对的，选D。
虽然这题的D选项带“均”，但由于公积金缴纳得多是积极的感情色彩，不能直接不看这个选项就说它错，计算发现，它居然是对的！